Situations canoniques généralisées

A - Situation grand-canonique

Elle correspond à l'étude d'un ``petit'' système noté $s$ en équilibre avec un réservoir $R$ d'énergie et de particules. Par conséquent, le nombre $N$ de particules de $s$ devient une variable interne, au même titre que son énergie. Nous allons donc attribuer à $s$ une distribution statistique, c'est-à-dire déterminer les différentes quantités $\overline{N}$, $\Delta N$, $\overline{E}$ et de $\Delta E$.

Bien entendu, le nombre de degrés de liberté $f_{s}$ du petit système est très petit devant celui de $R$, nous en tirons les inégalités $E \ll E_{R}$ et $N \ll N_{R}$. Nous supposerons de plus que le couplage entre $s$ et $R$ est faible et que le système $s \cup R$ est isolé, si bien que:

$$E_{0} \leq E + E_{R} \leq E_{0} + \delta E_{0}$$

$$N_{0} \leq N + N_{R} \leq N_{0} + \delta N_{0}$$

Mais il s'avère que la prise en compte simultanée de $\delta E_{0}$ et de $\delta N_{0}$ complique les calculs inutilement et aboutit aux mêmes résultats si l'on suppose que toute l'incertitude ne porte que sur $E_{0}$, énergie du système total isolé. Nous adopterons par la suite cette attitude et écrirons que:

$$E_{0} \leq E + E_{R} \leq E_{0} + \delta E_{0}$$ (6.1)

$$N + N_{R} = N_{0}$$ (6.2)

Remarque: Par rapport à la situation canonique où le réservoir d'énergie (le thermostat T) imposait sa température à $s$, la situation grand-canonique fait intervenir un réservoir d'énergie et de particules $R$, qui impose sa température et son potentiel chimique au petit système $s$: $T^{*} = T$ (condition d'équilibre thermique) et $\mu^{*} = \mu$ (condition d'équilibre osmotique).

Le développement de l'entropie microcanonique du réservoir donne ainsi:

$$S_{R}^{*}(E_{0}-E,N_{0}-N) \approx S_{R}^{*}(E_{0},N_{0}) - E{{\l... ...partial E}\right)}_{N}} - N\left(\frac{\partial S_{R}^{*}}{\partial N}\right)_E$$

d'où:

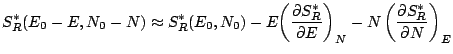
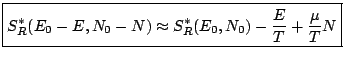$$\fbox{$\displaystyle S_{R}^{*}(E_{0}-E,N_{0}-N) \approx S_{R}^{*}(E_{0},N_{0}) - \frac{E}{T} + \frac{\mu}{T}N$}$$ (6.3)