Méthode des multiplicateurs de Lagrange

De même que pour les ensembles microcanonique et canonique, on peut utiliser le principe d'information minimum, lié à la maximisation de l'entropie statistique, pour obtenir la distribution grand-canonique des microétats du système étudié. Nous devons ainsi rechercher quand l'entropie d'information $$S = -k_{B}\sum_{\ell}{P_{\ell}\ln(P_{\ell})}$$ devient extremale, tenant compte des relations de contraintes:

$$\sum_{\ell}{P_{\ell}} = 1$$

$$\sum_{\ell}{P_{\ell}E_{\ell}} = \overline{E}$$

$$\sum_{\ell}{P_{\ell}N_{\ell}} = \overline{N}$$

Nous appliquons la méthode des multiplicateurs de Lagrange en recherchant l'extremum de la fonction:

$$L = -k_{B}\sum_{\ell}{P_{\ell}\ln(P_{\ell})} - \lambda_{1}\left(\... ...}\right) - \lambda_{3}\left(\sum_{\ell}{P_{\ell}N_{\ell}} - \overline{N}\right)$$

où $\lambda_{1}$, $\lambda_{2}$ et $\lambda_{3}$ sont les multiplicateurs de Lagrange respectivement associés aux trois contraintes précédentes.

Par conséquent, pour que L soit extremale il est nécessaire que

$$\forall{\ell}\ , \ \frac{\partial L}{\partial P_{\ell}} = 0$$

ce qui conduit à:

$$\forall{\ell}\ , \ -k_{B}\ln(P_{\ell}) - k_{B} - \lambda_{1} - \lambda_{2}E_{\ell} - \lambda_{3}N_{\ell} = 0$$

d'où:

$$P_{\ell} = e^{-1 - \frac{\lambda_{1}}{k_{B}}}\ \ e^{-\frac{\lambda_{2}}{k_{B}}E_{\ell} - \frac{\lambda_{3}}{k_{B}}N_{\ell}}$$

La condition de normalisation entraîne:

$$\sum_{\ell}{P_{\ell}} = 1\ \ \Rightarrow\ \ e^{-1 - \frac{\lambda... ...e^{-\frac{\lambda_{2}}{k_{B}}E_{\ell} - \frac{\lambda_{3}}{k_{B}}N_{\ell}}} = 1$$

donc:

$$e^{-1 - \frac{\lambda_{1}}{k_{B}}} = \frac{1}{\sum_{\ell}{e^{-\frac{\lambda_{2}}{k_{B}}E_{\ell} - \frac{\lambda_{3}}{k_{B}}N_{\ell}}}}$$

et ainsi:

$$\forall{\ell}\ , \ P_{\ell} = \frac{e^{-\frac{\lambda_{2}}{k_{B}}... ...l}{e^{-\frac{\lambda_{2}}{k_{B}}E_{\ell} - \frac{\lambda_{3}}{k_{B}}N_{\ell}}}}$$

La somme au dénominateur est une constante, nous la notons $\Xi$. Pour déterminer les valeurs de $\lambda_{2}$ et de $\lambda_{3}$, on repart de l'expression générale de S pour obtenir maintenant:

$$S = k_{B}\ln\Xi + \lambda_{2}\overline{E} + \lambda_{3}\overline{N}$$

Il vient donc, $\Xi$ étant constante:

$$\left(\frac{\partial S}{\partial \overline{E}}\right)_{V,\overline{N}} = \lambda_{2} = \frac{1}{T}$$

$$\left(\frac{\partial S}{\partial \overline{N}}\right)_{V,\overline{E}} = \lambda_{3} = -\frac{\mu}{T}$$

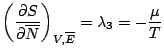
Nous retrouvons donc:

$$\forall{\ell}\ , \ P_{\ell} = \frac{1}{\Xi}e^{-\beta(E_{\ell} - \mu N_{\ell})}$$

avec:

$$\Xi = \sum_{\ell}{e^{-\beta(E_{\ell} - \mu N_{\ell})}}$$

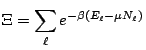
Ainsi, comme pour l'ensemble canonique, on constate que l'ensemble grand-canonique est adapté pour deux types de situations: d'une part les systèmes en équilibre avec un réservoir d'énergie et de particules, d'autre part les systèmes dont on connaît les valeurs moyennes de l'énergie et du nombre de particules. Là encore, on remarque que ces deux situations sont en réalité équivalentes car pour parvenir à fixer ces deux quantités, il faut justement mettre le système en contact avec un réservoir d'énergie et de particules.