Rappels des difficultés rencontrées au chapitre 4

En situation canonique, nous voulions calculer la fonction de partition canonique d'un ensemble de $N$ particules identiques, indépendantes et indiscernables, en équilibre thermique avec un thermostat:

$$Z(T,N) = \sum_{\{N_{\lambda}\}}{\exp(-\beta \sum_{\lambda}{N_{\lambda}\varepsilon_{\lambda}})}$$

avec la condition :

$$\sum_{\lambda}{N_{\lambda}} = N.$$

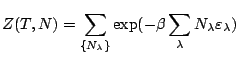
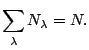
C'est cette condition qui nous a posé problème : les $N_{\lambda}$ n'étant pas indépendants, nous n'avions pas pu exprimer $Z(T,N)$ avec les fonctions de partition canoniques des particules individuelles. Dorénavant, nous supposons que $N$ est suffisament grand pour considérer que la limite thermodynamique est atteinte et exploiter l'équivalence des trois situations canoniques. En l'occurrence, nous allons utiliser les résultats de l'ensemble grand-canonique pour nous tirer d'affaire.