L'approximation de Maxwell-Boltzmann : limite commune des statistiques quantiques

Il s'agit ici d'examiner le cas où tous les nombres moyens d'occupation sont très petits devant 1. Ceci est possible si $\forall\lambda$, $e^{\beta(\varepsilon_{\lambda} - \mu)} \gg 1$, si bien que:

$$\overline{N_{\lambda}^{F}} \approx \overline{N_{\lambda}^{B}} \approx e^{-\beta(\varepsilon_{\lambda} - \mu)}$$

Dans cette limite commune, on ne parvient donc plus à distinguer fermions et bosons.

Recherche de $\mu$

$$\left. N \right. = \sum_{\lambda}{\overline{N_{\lambda}}}$$

$$= \sum_{\lambda}{e^{-\beta(\varepsilon_{\lambda} - \mu)}}$$

$$= e^{\beta\mu}\sum_{\lambda}{e^{-\beta\varepsilon_{\lambda}}}$$

$$\left. N \right. = e^{\beta\mu}z$$

soit finalement:

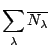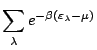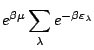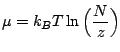$$\mu = k_{B}T\ln\Big(\frac{N}{z}\Big)$$ (6.44)

Calcul de Z

L'expression (6.41), désormais commune aux fermions et aux bosons, devient:

$$\left. \ln(Z) \right. \approx \sum_{\lambda}{e^{-\beta(\varepsilon_{\lambda} - \mu)}} - N\beta\mu$$

$$\left. \ln(Z) \right. \approx e^{\beta\mu}z - N\beta\mu$$

$$\approx N - N(\ln(N) - \ln(z))$$

$$\approx \ln(z^{N}) - (N\ln(N) - N)$$

$$\left. \ln(Z) \right. \approx \ln(z^{N}) - \ln(N!)$$

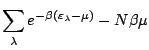D'où finalement:

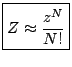$$\fbox{$\displaystyle Z \approx \frac{z^{N}}{N!}$}$$ (6.45)