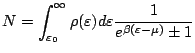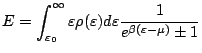Formules générales

Notre système

est maintenant quelconque (il n'est plus nécessairement macroscopique comme aux paragraphes précédents) mais en situation grand-canonique. A cause de l'indiscernabilité des particules, on ne peut pas attribuer à une particule un état propre individuel: nous devons ainsi exploiter les nombres d'occupation $N_{\lambda}$ , nombre de particules dans un état individuel $\phi_{\lambda}$ .

Remarque: Il ne faut pas confondre $\phi_{\lambda}$ , état propre pour une particule, avec $\phi_{\ell}$ , état propre pour le système de toutes les particules.

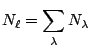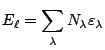Par conséquent, nous avons les relations: $\displaystyle N_{\ell} = \sum_{\lambda}{N_{\lambda}}$ et $\displaystyle E_{\ell} = \sum_{\lambda}{N_{\lambda}\varepsilon_{\lambda}}$ .

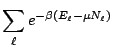$\displaystyle \left. \Xi \right.$	$\displaystyle =$	$\displaystyle \sum_{\ell}{e^{-\beta(E_{\ell} - \mu N_{\ell})}}$
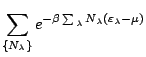$\displaystyle \left. \Xi \right.$	$\displaystyle =$	$\displaystyle \sum_{\{N_{\lambda}\}}{e^{-\beta\sum_{\lambda}{N_{\lambda}(\varepsilon_{\lambda} - \mu)}}}$

La somme précédente porte sur les configurations $\{N_{\lambda}\}$ , on peut la décomposer en un produit de sommes indépendantes sous la forme:

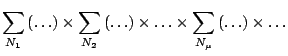
$\displaystyle \sum_{N_{1}}{(\ldots)}\times\sum_{N_{2}}{(\ldots)}\times\ldots\times\sum_{N_{\mu}}{(\ldots)}\times\ldots$

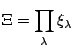$\displaystyle \Xi = \prod_{\lambda}{\xi_{\lambda}}$

(6.34)

$\displaystyle \xi_{\lambda} = \sum_{N_{\lambda}}{e^{-\beta N_{\lambda}(\varepsilon_{\lambda} - \mu)}}$

(6.35)

Nous venons donc de décomposer la grande fonction de partition $\Xi$ en un produit de grandes fonctions de partition relatives aux différents états individuels $\phi_{\lambda}$ . Par suite,

$\displaystyle \left. J \right.$	$\displaystyle =$	$\displaystyle -k_{B}T\ln\Xi$
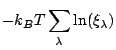$\displaystyle \left. J \right.$	$\displaystyle =$	$\displaystyle -k_{B}T\sum_{\lambda}{\ln(\xi_{\lambda})}$

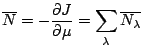
$\displaystyle \overline{N} = -\frac{\partial J}{\partial\mu} = \sum_{\lambda}{\overline{N_{\lambda}}}$

$\displaystyle \fbox{$\displaystyle \overline{N_{\lambda}} = k_{B}T\frac{\partial}{\partial\mu}\ln(\xi_{\lambda})$}$

(6.36)

$\displaystyle N = \overline{N} = \sum_{\lambda}{\overline{N_{\lambda}}}$

(6.37)

$\displaystyle E = \overline{E} = \sum_{\lambda}{\overline{N_{\lambda}}\varepsilon_{\lambda}}$

(6.38)

A partir de ces deux relations, on peut avoir accès à toutes les propriétés thermodynamiques du système :

...

Remarque: lorsque l'approximation continue est valide, (6.37) et (6.38) deviennent respectivement:

$\displaystyle N = \int_{\varepsilon_{0}}^{\infty}{\rho(\varepsilon)d\varepsilon\frac{1}{e^{\beta (\varepsilon - \mu)} \pm 1}}$

$\displaystyle E = \int_{\varepsilon_{0}}^{\infty}{\varepsilon\rho(\varepsilon)d\varepsilon\frac{1}{e^{\beta (\varepsilon - \mu)} \pm 1}}$