Nous n'utiliserons ici que le principe fondamental pour établir cette distribution. Soit ![]() la probabilité de trouver
la probabilité de trouver ![]() dans le microétat
dans le microétat
![]() , correspondant à l'énergie
, correspondant à l'énergie ![]() et au volume
et au volume ![]() , quel que soit par ailleurs l'état dans lequel se trouve
, quel que soit par ailleurs l'état dans lequel se trouve ![]() , pourvu que les relations (6.25) et (6.26) soient satisfaites. Comme en situation grand-canonique, l'application du principe fondamental à
, pourvu que les relations (6.25) et (6.26) soient satisfaites. Comme en situation grand-canonique, l'application du principe fondamental à ![]() isolé donne
isolé donne
![]() . Par ailleurs,
. Par ailleurs,
![]() ; l'approximation (6.27) fournit ainsi:
; l'approximation (6.27) fournit ainsi:
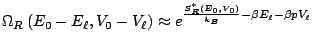
 |
(6.28) |
Remarque:
![]() possède plusieurs expressions selon que l'approximation continue est valide ou non:
possède plusieurs expressions selon que l'approximation continue est valide ou non:
