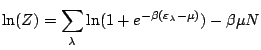D'après le principe d'exclusion de Pauli:
![]() ,
,
![]() ou
ou ![]() . D'après (6.35), nous avons donc:
. D'après (6.35), nous avons donc:
| (6.39) |
On en déduit
![]() à partir de (6.36):
à partir de (6.36):
 |
(6.40) |
En outre, on remarquera que:

Expression de Z:
Pour cela, on utilise l'expression du grand potentiel:

De plus,
![]() à la limite thermodynamique et
à la limite thermodynamique et
![]() .
Par conséquent, nous obtenons la relation générale pour
.
Par conséquent, nous obtenons la relation générale pour ![]() :
:
soit finalement: