La probabilité ![]() que le petit système
que le petit système ![]() se trouve dans le microétat
se trouve dans le microétat
![]() d'énergie
d'énergie ![]() , quel que soit par ailleurs l'état dans lequel se trouve le thermostat - pourvu que (4.1) soit vérifiée - est:
, quel que soit par ailleurs l'état dans lequel se trouve le thermostat - pourvu que (4.1) soit vérifiée - est:
 |
|||
 |
D'où
![]() .
.
Nous étudions plutôt
![]() et pour cela on développe cette quantité au premier ordre4.1:
et pour cela on développe cette quantité au premier ordre4.1:
![$\displaystyle \ln \Omega_{T}(E_{0}) - \ln \Omega_{s\cup T}(E_0)\ - E_{\ell}\lef...
...c{\partial}{\partial E_{T}}\ln \Omega_{T}\right]_{E_{0}} + {\cal O}(E_{\ell}^2)$](img676.png) |
Or:
![$\displaystyle \left. \left[\frac{\partial}{\partial E_{T}}\ln \Omega_{T}\right]_{E_{0}}
\right.$](img677.png) |
![$\displaystyle \frac{1}{k_{B}}\left[\frac{\partial}{\partial E_{T}}(k_{B}\ln\Omega_{T})\right]_{E_{0}}$](img678.png) |
||
![$\displaystyle \frac{1}{k_{B}}\left[\frac{\partial S^{*}}{\partial E_{T}}\right]_{E_{0}} = \frac{1}{k_{B}T_{T}^{*}(E_{0})}$](img679.png) |
|||
D'où

soit:
La probabilité ![]() que
que ![]() occupe le microétat
occupe le microétat ![]() est donc proportionnelle au facteur de Boltzmann
est donc proportionnelle au facteur de Boltzmann
![]() . Nous posons alors
. Nous posons alors
![]() ; la condition de normalisation
; la condition de normalisation
![]() donne:
donne:
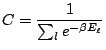
Nous introduisons la fonction de partition ![]() du système étudié par:
du système étudié par:
La probabilité d'occupation du microétat
![]() est finalement:
est finalement:
 |
(4.4) |
Justifions à présent que l'on pouvait négliger le terme d'ordre deux dans le développement limité de
![]() ; pour cela, nous évaluons le quotient des termes d'ordre deux et d'ordre un:
; pour cela, nous évaluons le quotient des termes d'ordre deux et d'ordre un:
 |
 |
||
 |
|||
 |
|||
 or or
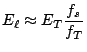 d'après (3.10) d'après (3.10) |
|||
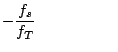 |
Il était donc licite de se contenter du terme d'ordre un dans le développement limité précédent.