![\includegraphics[width=5cm]{micro_sssyst_isole.eps}](img544.png)
![\includegraphics[width=5cm]{micro_sssyst_isole.eps}](img544.png)
Soit ![]() un système isolé de l'extérieur par une paroi isolante et soit
un système isolé de l'extérieur par une paroi isolante et soit ![]() et
et ![]() deux sous-systèmes de
deux sous-systèmes de ![]() - voir figure ci-contre -. Les deux sous-systèmes étant initialement à l'équilibre, nous rendons la paroi les séparant diatherme: nous cherchons ainsi à déterminer quand l'équilibre thermique entre
- voir figure ci-contre -. Les deux sous-systèmes étant initialement à l'équilibre, nous rendons la paroi les séparant diatherme: nous cherchons ainsi à déterminer quand l'équilibre thermique entre ![]() et
et ![]() est de nouveau atteint. Les échanges thermiques entre les deux sous-systèmes implique d'une part la présence d'un faible terme de couplage dans l'hamiltonien du système total isolé:
est de nouveau atteint. Les échanges thermiques entre les deux sous-systèmes implique d'une part la présence d'un faible terme de couplage dans l'hamiltonien du système total isolé:
![]() , d'autre part le fait que
, d'autre part le fait que ![]() et
et ![]() sont des variables internes alors que
sont des variables internes alors que
![]() est un paramètre extérieur, connu à
est un paramètre extérieur, connu à ![]() près. On rappelle à ce propos l'inégalité suivante:
près. On rappelle à ce propos l'inégalité suivante:
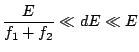
Deux calculs sont succeptibles de nous intéresser:
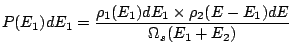
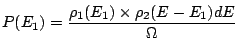 |
(3.8) |
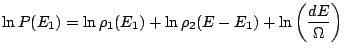
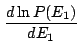 |
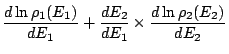 |
||
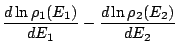 car car
|
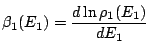 et
et 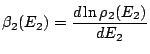 . Ainsi,
. Ainsi,
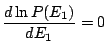 , i.e.:
, i.e.:
Remarque: On a vu au chapitre précédent que
![]() . Donc
. Donc
![]() et finalement:
et finalement:
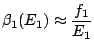
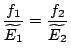 , c'est-à-dire qu'à l'équilibre thermique, les deux sous-systèmes
, c'est-à-dire qu'à l'équilibre thermique, les deux sous-systèmes 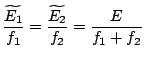 , si bien que:
, si bien que:
Définition: On définit la température microcanonique ![]() d'un système isolé à l'équilibre par:
d'un système isolé à l'équilibre par:
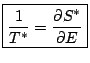 |
(3.11) |
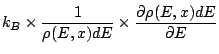 |
|||
 |
|||
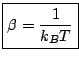 |
(3.12) |
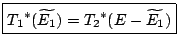 |
(3.13) |
Nous allons maintenant établir la loi d'évolution de ![]() en fonction de
en fonction de ![]() . Pour cela, on développe la quantité
. Pour cela, on développe la quantité
![]() au voisinage de
au voisinage de
![]() :
:
Remarque: justifions que
![]() correspond à un maximum - et non à un minimum - de
correspond à un maximum - et non à un minimum - de ![]() . Pour ce faire, déterminons le signe de la dérivée seconde dans le développement ci-dessus:
. Pour ce faire, déterminons le signe de la dérivée seconde dans le développement ci-dessus:
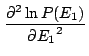 |
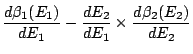 |
||
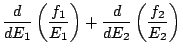 |
|||
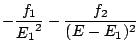 |
Finalement,
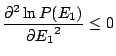 , ce qui prouve que
, ce qui prouve que ![]() atteint son maximum en
atteint son maximum en
![]() . Poursuivons encore le calcul précédent:
. Poursuivons encore le calcul précédent:
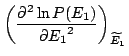 |
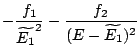 |
||
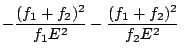 car car
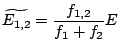 |
|||
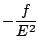 en posant en posant
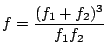 |
En réinjectant la dernière égalité dans (3.14), nous obtenons finalement:
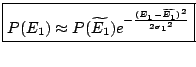 |
(3.15) |
 .
.
La distribution de probabilité ![]() est donc approximativement une gaussienne centrée sur
est donc approximativement une gaussienne centrée sur
![]() et d'écart quadratique moyen
et d'écart quadratique moyen
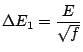 . Déterminons à présent l'amplitude relative des fluctuations de
. Déterminons à présent l'amplitude relative des fluctuations de ![]() autour de sa valeur la plus probable
autour de sa valeur la plus probable
![]() :
:
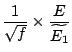 |
|||
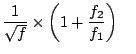 d'après (3.10) d'après (3.10) |
|||
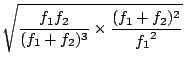 |
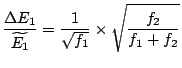 |
(3.16) |
Ainsi, même dans le cas limite où
![]() - cas de la situation canonique - nous avons encore
- cas de la situation canonique - nous avons encore
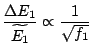 , avec
, avec ![]() de l'ordre de
de l'ordre de ![]() .
.
Conséquence: l'amplitude relative des fluctuations de ![]() autour de
autour de
![]() est tellement faible devant 1 que nous pouvons assimiler la distribution de probabilité
est tellement faible devant 1 que nous pouvons assimiler la distribution de probabilité ![]() à un pic de Dirac centré sur
à un pic de Dirac centré sur
![]() , aussi valeur moyenne de
, aussi valeur moyenne de ![]() . En d'autres termes, notre gaussienne est si étroite que
. En d'autres termes, notre gaussienne est si étroite que
![]() est la seule valeur possible pour
est la seule valeur possible pour ![]() , de même
, de même
![]() pour
pour ![]() . Ce sont du moins les valeurs obtenues lorsque l'équilibre thermique entre les deux sous-systèmes est de nouveau atteint. D'un point de vue plus physique, les deux sous-systèmes ont ainsi échangé de l'énergie jusqu'à équilibrer leur température: le sous-système ayant initialement la température la plus élevée a perdu de l'énergie au profit de l'autre sous-système qui a donc vu sa température augmenter.
. Ce sont du moins les valeurs obtenues lorsque l'équilibre thermique entre les deux sous-systèmes est de nouveau atteint. D'un point de vue plus physique, les deux sous-systèmes ont ainsi échangé de l'énergie jusqu'à équilibrer leur température: le sous-système ayant initialement la température la plus élevée a perdu de l'énergie au profit de l'autre sous-système qui a donc vu sa température augmenter.