Méthode des multiplicateurs de Lagrange

L'objectif est de retrouver, pour les systèmes dont l'énergie moyenne est fixée, la distribution canonique des microétats, par le biais de notions de théorie de l'information (méthode des multiplicateurs de lagrange).

Soit de nouveau $P_{\ell}$ la probabilité d'occuper le microétat $\phi_{\ell}$: à l'équilibre, l'entropie d'information $S = -k_B\sum_{\ell}{P_{\ell} \ln(P_{\ell})}$ doit être maximale. Nous devons de plus tenir compte des deux relations de contrainte qui nous sont imposées: d'une part la condition de normalisation $\sum_{\ell} {P_{\ell}} = 1$, d'autre part le fait que l'énergie moyenne du système est fixée: $\sum_{\ell}{P_{\ell} E_{\ell}} = \overline{E_c}$.

Pour appliquer la méthode des multiplicateurs de Lagrange, il faut chercher le maximum de la fonction:

$$L(P_{\ell}) = S - \lambda_1 \left(\sum_{\ell}{P_{\ell}} - 1\right) - \lambda_2 \left(\sum_{\ell}{P_{\ell} E_{\ell}} - \overline{E_c}\right)$$

où $\lambda_1$ et $\lambda_2$ sont les multiplicateurs de Lagrange associés aux deux relations de contrainte définies précédemment. Pour que $L$ soit maximale, il est nécessaire que:

$$\forall \ell, ~\frac{\partial L}{\partial P_{\ell}} = 0$$

c'est-à-dire:

$$\forall \ell, ~-k_B \ln(P_{\ell}) - k_B - \lambda_1 - \lambda_2 E_{\ell} = 0$$

donc:

$$\forall \ell, ~P_{\ell} = e^{-1-\frac{\lambda_1}{k_B}} ~e^{-\frac{\lambda_2}{k_B} E_{\ell}}$$

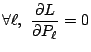
Par ailleurs, la condition de normalisation donne:

$$e^{-1-\frac{\lambda_1}{k_B}} = \frac{1}{\sum_{\ell}{e^{-\frac{\lambda_2}{k_B} E_{\ell}}}}$$

d'où, en introduisant la fonction de partition $Z$ du système comme en (4.3), nous obtenons:

$$\displaystyle \forall{\ell}, ~P_{\ell} = \frac{e^{-\frac{\lambda_2}{k_B} E_{\ell}}}{Z}$$

Reste à exploiter la seconde relation de contrainte; pour cela, on repart de l'expression de l'entropie:

$$\left. S \right. = -k_B \sum_{\ell} {P_{\ell} \ln(P_{\ell})}$$

$$= -k_B \sum_{\ell}\left({\frac{e^{-\frac{\lambda_2}{k_B} E_{\ell}}}{Z}\times\left[-\frac{\lambda_2}{k_B}E_{\ell} - \ln(Z)\right]}\right)$$

$$= k_B \ln(Z) + \lambda_2 \overline{E_c}$$

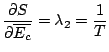Ainsi,  $$\frac{\partial S}{\partial \overline{E_c}} = \lambda_2 = \frac{1}{T}$$, nous retrouvons donc la distribution canonique des microétats occupés par le système:

$$P_{\ell} = \frac{e^{-\frac{E_{\ell}}{k_B T}}}{Z}$$ (4.5)

La distribution canonique s'applique donc a priori dans deux situations: pour les systèmes en contact thermique avec un thermostat et pour les systèmes dont l'énergie moyenne est fixée. Toutefois, pour fixer l'énergie moyenne d'un système, il est nécessaire de le mettre en contact avec un thermostat: ces deux situations sont donc les mêmes en pratique.

Il est important de retenir que, contrairement à la situation microcanonique, les microétats accessibles au système en situation canonique ne sont pas équiprobables: de par la présence du facteur de Boltzmann $$e^{-\frac{E_{\ell}}{k_B T}}$$, les microétats les plus probables, à température fixée, sont ceux de plus faible énergie.