Nous allons montrer que la fonction de partition ![]() donne accès à toutes les propriétés thermodynamiques du système en situation canonique. On lui préfère souvent, par commodité, une grandeur thermodynamique appelée énergie libre, notée
donne accès à toutes les propriétés thermodynamiques du système en situation canonique. On lui préfère souvent, par commodité, une grandeur thermodynamique appelée énergie libre, notée ![]() , définie par:
, définie par:
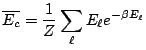 , mais d'après (4.3),
, mais d'après (4.3),
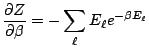 , donc
, donc
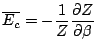 . Finalement, l'énergie moyenne du système en situation canonique est:
. Finalement, l'énergie moyenne du système en situation canonique est:
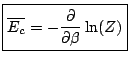 |
(4.16) |
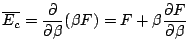 et
et
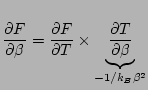 soit:
soit:
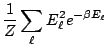 |
|||
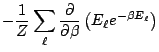 |
|||
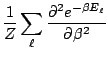 |
|||
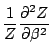 |
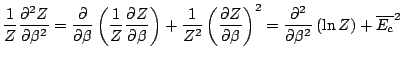 .
.
D'où l'expression de l'écart type énergétique:
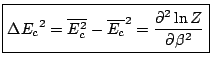 |
(4.18) |
On remarquera en outre que
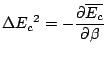 .
.
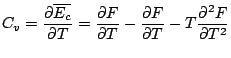 donc:
donc:
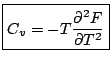 |
(4.19) |
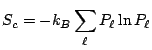 avec
avec
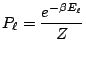 . Ainsi:
. Ainsi:
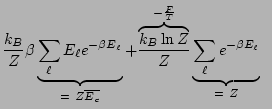 , or , or
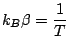 |
|||
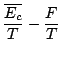 |
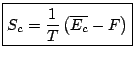 |
(4.20) |
Reste à identifier cette dernière relation avec (4.17) pour obtenir que:

Pour la pression et le potentiel chimique canoniques, on les définit de la façon suivante:
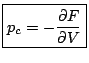 |
(4.21) |
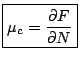 |
(4.22) |