Le petit système ![]() est supposé être à l'équilibre. On décide de relacher une contrainte et l'on cherche à déterminer quand
est supposé être à l'équilibre. On décide de relacher une contrainte et l'on cherche à déterminer quand ![]() atteint de nouveau un état équilibre. Considérons pour cela le système total isolé constitué de
atteint de nouveau un état équilibre. Considérons pour cela le système total isolé constitué de ![]() et de
et de ![]() . La probabilité pour que
. La probabilité pour que ![]() se trouve dans les microétats
se trouve dans les microétats
![]() pour
pour ![]() et
et ![]() pour
pour ![]() est:
est:
![]() . L'entropie de
. L'entropie de ![]() est alors:
est alors:
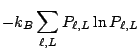 |
|||
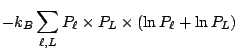 |
|||
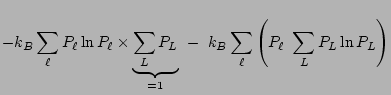 |
|||
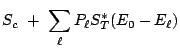 |
On a vu en 4.1.1 que
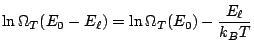 à l'ordre deux en
à l'ordre deux en
![]() près, on peut donc considérer que
près, on peut donc considérer que
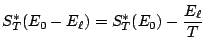 . D'où:
. D'où:
 |
|||
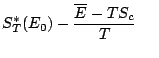 i.e. i.e. |
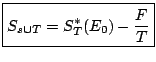 |
(4.23) |
Or l'évolution spontanée de ![]() s'accompagne nécessairement de l'augmentation de l'entropie du système total isolé: dans la mesure où
s'accompagne nécessairement de l'augmentation de l'entropie du système total isolé: dans la mesure où
![]() et
et ![]() sont constantes, l'énergie libre
sont constantes, l'énergie libre ![]() du petit système ne peut que diminuer. Le nouvel état d'équilibre est donc atteint lorsque
du petit système ne peut que diminuer. Le nouvel état d'équilibre est donc atteint lorsque ![]() devient minimale, toutes les autres contraintes demeurant satisfaites.
devient minimale, toutes les autres contraintes demeurant satisfaites.