A partir de l'expression de ![]() déterminée précédemment, l'entropie microcanonique, que l'on note
déterminée précédemment, l'entropie microcanonique, que l'on note ![]() , est égale à:
, est égale à:
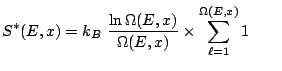 soit:
soit:
| (3.3) |
D'après (3.1), nous avons encore:
Nous pouvons réécrire cette dernière relation:
![$\displaystyle S^* (E,x) = k_B \ln\left[\rho(E,x)\times\varepsilon\times\frac{dE}{\varepsilon}\right]$](img532.png)
![$\displaystyle k_B \ln \left[\rho(E,x)\varepsilon\right] + k_B \ln\left(\frac{dE}{E}\times f\right)$](img535.png) |
|||
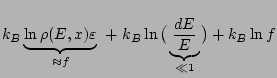 |
![]() étant de l'ordre du nombre d'Avogadro, le premier terme de l'expression précédente est généralement prépondérant sur les deux autres et ainsi:
étant de l'ordre du nombre d'Avogadro, le premier terme de l'expression précédente est généralement prépondérant sur les deux autres et ainsi:
| (3.5) |
Cette dernière relation est importante car elle indique que l'entropie microcanonique ![]() ne dépend plus de
ne dépend plus de ![]() . On peut même aller plus loin dans les approximations en partant de (3.4) et en prenant le logarithme népérien de quantités dimensionnées:
. On peut même aller plus loin dans les approximations en partant de (3.4) et en prenant le logarithme népérien de quantités dimensionnées:
Ainsi, parce que
![]() , nous obtenons:
, nous obtenons:
| (3.6) |
Enfin, étant donné que
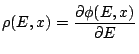 , nous déduisons de même:
, nous déduisons de même:
| (3.7) |