Méthode des multiplicateurs de Lagrange

Si l'on a quelques réticences à admettre le principe fondamental, on peut toujours retrouver la distribution microcanonique par la méthode des multiplicateurs de Lagrange. Considérons l'entropie $S$ de notre système isolé: $S = -k_B \sum_{\ell} {P_{\ell} \ln P_{\ell}}$. Nous cherchons à déterminer le maximum de $S$ par rapport aux $P_{\ell}$ tout en satisfaisant à la relation de contrainte $\sum_{\ell} {P_{\ell}} = 1$.

Soit donc $$L(P_{\ell}) = S - \lambda_1 \Big(\sum_{\ell} {P_{\ell}} - 1\Big)$$ où $\lambda_1$ est le multiplicateur de Lagrange associé à la relation de contrainte ci-dessus. Ainsi:

$$\left. \forall{\ell}, ~\frac{\partial L(P_{\ell})}{\partial P_{\ell}} = 0 \right. \Leftrightarrow \forall{\ell}, ~\frac{\partial}{\partial P_{\ell}}\left(-k_B P_{\ell} \ln P_{\ell} - \lambda_1 P_{\ell} + \lambda_1\right)$$

$$\Leftrightarrow \forall{\ell}, ~-k_B \ln P_{\ell} - k_B - \lambda_1 = 0$$

$$\Leftrightarrow \forall{\ell}, ~P_{\ell} = e^{-\frac{\lambda_1}{k_B} - 1}$$

Puis $$\sum_{\ell = 1}^{\Omega(E,x)} {P_{\ell}} = e^{-\frac{\lambda_1}{k_B} - 1}\times\underbrace{\sum_{\ell = 1}^{\Omega(E,x)} {1}}_{\Omega(E,x)} = 1$$.

D'où finalement:

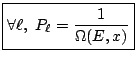
On retrouve bien le fait que tous les microétats accessibles au système en situation microcanonique sont équiprobables.