




suivant: Généralisation à N particules
monter: Particules libres enfermées dans
précédent: Particules libres enfermées dans
Table des matières
Index
Pour aboutir à l'expression de la densité d'état, il nous faut effectuer le traitement quantique d'une particule piégée à l'intérieur d'une boîte. Deux méthodes sont généralement employées: la méthode des conditions aux limites strictes et la méthode des conditions aux limites périodiques.
a) Conditions aux limites strictes
- -
- A une dimension: il nous faut résoudre l'équation de Schrödinger
[4]stationnaire
 . Ses solutions sont de la forme
. Ses solutions sont de la forme
[4]
 où
où
 . Notre particule étant confinée dans un puits de potentiel unidimensionnel de largeur
. Notre particule étant confinée dans un puits de potentiel unidimensionnel de largeur  , de profondeur infinie, la méthode des conditions aux limites strictes impose que
, de profondeur infinie, la méthode des conditions aux limites strictes impose que
 . Il est alors facile d'obtenir l'expression des états propres et des énergies propres:
où
. Il est alors facile d'obtenir l'expression des états propres et des énergies propres:
où  est un entier naturel non-nul défini par
est un entier naturel non-nul défini par
 .
.
- -
- A trois dimensions: la généralisation est immédiate; en effet, la particule étant libre dans la boîte, son hamiltonien est à variables séparables: l'énergie totale à trois dimensions est la somme des énergies à une dimension de même que l'état propre correspondant à trois dimensions est le produit des états propres à une dimension. En somme, nous obtenons:
avec
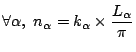 et
et
 . On remarquera en outre que l'énergie totale de la particule s'écrit:
. On remarquera en outre que l'énergie totale de la particule s'écrit:
 |
(2.10) |
- -
- Calcul de
 :
:
Figure 2.1:
Microétats accessibles dans l'espace des vecteurs d'onde.
|
|
On se place dans l'espace des vecteurs d'onde: les microétats accessibles au système sont représentés par les sommets des parallélépipèdes élémentaires de côtés
 et
et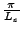 à la figure 2.1, page
à la figure 2.1, page ![[*]](file:/usr/lib/latex2html/icons/crossref.png) . Or d'après (
. Or d'après (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ), nous avons:
ce qui laisse penser que les microétats accessibles au système sont compris, dans l'espace des vecteurs d'onde, dans la sphère de centre l'origine et de rayon
), nous avons:
ce qui laisse penser que les microétats accessibles au système sont compris, dans l'espace des vecteurs d'onde, dans la sphère de centre l'origine et de rayon
 . Néanmoins, il faut garder à l'esprit que
. Néanmoins, il faut garder à l'esprit que  ,
,  et
et  sont des entiers naturels non-nuls, donc
sont des entiers naturels non-nuls, donc  ,
,  et
et  sont strictement positifs. Ainsi, les microétats accessibles ne sont contenus que dans le huitième de cette sphère. Enfin, le volume d'un parallélépipède élémentaire étant égal à
sont strictement positifs. Ainsi, les microétats accessibles ne sont contenus que dans le huitième de cette sphère. Enfin, le volume d'un parallélépipède élémentaire étant égal à
 , nous déduisons l'expression de
, nous déduisons l'expression de  (quotient du volume accessible dans l'espace des
(quotient du volume accessible dans l'espace des  par le volume d'un parallélépipède élémentaire de cet espace):
par le volume d'un parallélépipède élémentaire de cet espace):
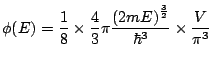
, soit:
 |
(2.11) |
- -
- Calcul de
 : Il ne reste plus qu'à dériver l'équation précédente:
: Il ne reste plus qu'à dériver l'équation précédente:
 |
(2.12) |
Remarque: Nous avons négligé les effets de bord dans le calcul de  - prise en compte de
- prise en compte de  ,
,  et
et  nuls - ce qui est licite dans la mesure où le rayon de la sphère accessible dans l'espace des
nuls - ce qui est licite dans la mesure où le rayon de la sphère accessible dans l'espace des  est très grand devant le côté d'un parallélépipède élémentaire.
est très grand devant le côté d'un parallélépipède élémentaire.
b) Conditions aux limites périodiques
Par rapport au traitement quantique précédent, la seule différence est qu'on impose l'égalité entre  et
et  sans pour autant imposer que ces deux termes soient nuls: c'est la condition de Born - Van Karman. La résolution de l'équation de Schrödinger stationnaire donne désormais pour solutions les ondes planes
sans pour autant imposer que ces deux termes soient nuls: c'est la condition de Born - Van Karman. La résolution de l'équation de Schrödinger stationnaire donne désormais pour solutions les ondes planes
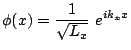 avec cette fois-ci
avec cette fois-ci
 ,
,  entier relatif et non plus entier naturel non-nul. A une dimension, l'énergie de la particule s'écrit toujours:
entier relatif et non plus entier naturel non-nul. A une dimension, l'énergie de la particule s'écrit toujours:
A trois dimensions, la généralisation est encore immédiate:
avec
 . Là encore, on remarque que l'énergie de la particule est donnée par (
. Là encore, on remarque que l'énergie de la particule est donnée par (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ), et que
), et que
 . Comme les
. Comme les
 sont des entiers relatifs quelconques, les microétats accessibles au système sont cette fois-ci contenus dans toute la sphère de centre l'origine et de rayon
sont des entiers relatifs quelconques, les microétats accessibles au système sont cette fois-ci contenus dans toute la sphère de centre l'origine et de rayon
 et non plus seulement dans son huitième comme précédemment. Cependant, ce facteur est compensé par le fait que le volume d'un parallélépipède élémentaire est désormais de
et non plus seulement dans son huitième comme précédemment. Cependant, ce facteur est compensé par le fait que le volume d'un parallélépipède élémentaire est désormais de
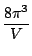 . On retrouve donc comme prévu les mêmes expressions pour
. On retrouve donc comme prévu les mêmes expressions pour  et
et  que dans le cas des conditions aux limites strictes.
que dans le cas des conditions aux limites strictes.





suivant: Généralisation à N particules
monter: Particules libres enfermées dans
précédent: Particules libres enfermées dans
Table des matières
Index
Clément Baruteau
2003-04-30
 . Ses solutions sont de la forme
. Ses solutions sont de la forme
 . Notre particule étant confinée dans un puits de potentiel unidimensionnel de largeur
. Notre particule étant confinée dans un puits de potentiel unidimensionnel de largeur 
 .
.


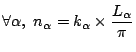 et
et

 . Néanmoins, il faut garder à l'esprit que
. Néanmoins, il faut garder à l'esprit que 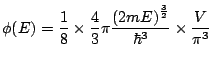 , soit:
, soit:
![]() - prise en compte de
- prise en compte de ![]() ,
, ![]() et
et ![]() nuls - ce qui est licite dans la mesure où le rayon de la sphère accessible dans l'espace des
nuls - ce qui est licite dans la mesure où le rayon de la sphère accessible dans l'espace des ![]() est très grand devant le côté d'un parallélépipède élémentaire.
est très grand devant le côté d'un parallélépipède élémentaire.




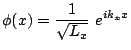 avec cette fois-ci
avec cette fois-ci
 ,
, 


 . Là encore, on remarque que l'énergie de la particule est donnée par (
. Là encore, on remarque que l'énergie de la particule est donnée par ( . Comme les
. Comme les