Expression des diverses grandeurs physiques

a)

Calcul de $E$:

Calculons d'abord l'énergie moyenne du système, dans le cas particulier de bosons de spin nul:

$$\left. E \right. = \frac{V}{h^{3}}\int_0^{\infty}{\frac{\varepsilon}{e^{\beta\varepsilon} - 1}d\varepsilon}$$

$$= \frac{4\pi V}{h^{3}}\int_{0}^{\infty}{\frac{p^{2}/2m}{e^{\beta p^{2}/2m} - 1}p^{2}dp}$$

$$= \frac{8\pi Vm^{2}}{h^{3}\sqrt{2m}}\int_{0}^{\infty}{\frac{u^{\frac{3}{2}}du}{e^{\beta u} - 1}}$$

$$= \frac{8\pi Vm^{\frac{3}{2}}}{h^{3}\sqrt{2}}(k_{B}T)^{\frac{5}{2}}... ...nfty}{\frac{x^{\frac{3}{2}}dx}{e^{x} - 1}}}_{\frac{3\sqrt{\pi}}{4}\times 1,341}$$

$$= \frac{3}{2}\times 1,341 \frac{V}{\Lambda^{3}(T)}(k_{B}T)$$

$$\left. E \right. = \frac{3}{2}\times 1,341 \frac{N}{\Lambda^{3}(T)}(k_{B}T)\underbrace{\frac{\Lambda^{3}(T_{B})}{\zeta(\frac{3}{2})}}_{=\frac{V}{N}}$$

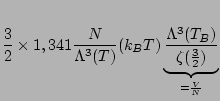D'où finalement:

$$\fbox{$\displaystyle E = 0,77Nk_{B}T\left(\frac{T}{T_{B}}\right)^{\frac{3}{2}}$}$$ (8.9)

b)

Calcul de $C_v$:

Par suite, nous en déduisons $C_{v}(T)$:

$$\left. C_{v}(T) \right. = \frac{\partial E}{\partial T}$$

$$\left. C_{v}(T) \right. = 0,77 Nk_{B}T_{B}^{-\frac{3}{2}}\times\frac{5}{2}T^{\frac{3}{2}}$$

Soit:

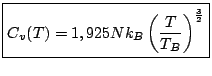$$\fbox{$\displaystyle C_{v}(T) = 1,925Nk_{B}\left(\frac{T}{T_{B}}\right)^{\frac{3}{2}}$}$$ (8.10)

Il importe ici de souligner la dépendance en température de la capacité thermique à volume constant du gaz de bosons, en comparaison avec le gaz parfait classique pour lequel $C_{v} = \frac{3}{2}R$ est indépendante de T.

c)

Calcul de $J$:

D'après (8.3), nous avons:

$$\left. J \right. = k_{B}T\int_{0}^{\infty}{\rho(\varepsilon)\ln(1 - e^{-\beta (\varepsilon - \mu)})d\varepsilon}$$

$$= k_B T AV\int_{0}^{\infty}{\sqrt{\varepsilon}\ln(1 - e^{-\beta (\varepsilon - \mu)})d\varepsilon}$$

$$= k_B T AV\Big\{\underbrace{\left[\frac{2}{3}\varepsilon^{\frac{3}{... ...\frac{\varepsilon^{\frac{3}{2}}d\varepsilon}{e^{\beta(\varepsilon - \mu)} - 1}}$$

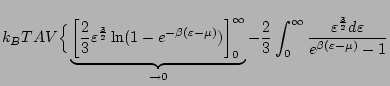i.e.:

$$\fbox{$\displaystyle J = -\frac{2}{3}E$}$$ (8.11)

d)

Calcul de $F$:

Dans le cadre de la condensation de Bose - Einstein, la potentiel chimique $\mu$ est nul pour $T \leq T_B$. Par conséquent, la limite thermodynamique étant atteinte, nous avons simplement:

$$\fbox{$\displaystyle F = J = -\frac{2}{3}E$}$$ (8.12)

e)

Calcul de $S$:

Nous avons $$S = -\frac{\partial F}{\partial T}$$ d'ou:

$$\left. S \right. = \frac{2}{3}\frac{\partial E}{\partial T}$$

$$= \frac{2}{3}\times\frac{5}{2}\frac{E}{T}$$

donc:

$$\fbox{$\displaystyle S = \frac{5}{3}\frac{E}{T}$}$$ (8.13)

f)

Calcul de $P$ et équation d'état:

$$\left. P \right. = -\frac{\partial F}{\partial V}$$

$$= \frac{2}{3}\frac{\partial E}{\partial V}$$

donc:

$$\fbox{$\displaystyle P = \frac{2}{3}\frac{E}{V}$}$$ (8.14)

Il s'agit de l'équation d'état du gaz de bosons en condensation de Bose - Einstein, c'est-à-dire pour $T \leq T_B$. De plus, (8.14) s'écrit encore:

$$P = 1,341(2s+1)\left(\frac{m}{2\pi\hbar^2}\right)^{\frac{3}{2}}\left(k_B T\right)^{\frac{5}{2}}$$ (8.15)

Autrement dit, la pression obtenue avec la condensation de Bose - Einstein ne dépend pas du volume ni du nombre de particule, mais seulement de la température.