Nous sommes dans le cas où la température T du système est strictement inférieure à température de Bose ![]() ou, ce qui revient au même, que
ou, ce qui revient au même, que
![]() . On a:
. On a:
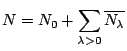 |
(8.7) |
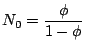 .
.
L'astuce consiste alors à admettre que:
D'où:
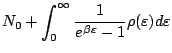 |
|||
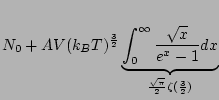 |
|||
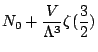 |
Par conséquent, la fraction d'atomes dans le niveau fondamental est:
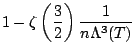 |
|||
![$\displaystyle 1 - \left[\frac{\Lambda(T_{B})}{\Lambda(T)}\right]^{3}$](img1439.png) |
car
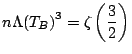 . Puisque
. Puisque
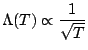 , on a finalement:
, on a finalement:
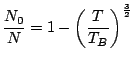 |
(8.8) |
Ainsi, pour ![]() , un nombre macroscopique de bosons va occuper le niveau fondamental: c'est la condensation de Bose - Einstein. Il est important de bien comprendre que pour
, un nombre macroscopique de bosons va occuper le niveau fondamental: c'est la condensation de Bose - Einstein. Il est important de bien comprendre que pour ![]() , les bosons sont tous excités et ne peuplent pas l'état fondamental, impliquant
, les bosons sont tous excités et ne peuplent pas l'état fondamental, impliquant ![]() . Pour
. Pour ![]() , c'est le début de condensation de Bose - Einstein: les niveaux excités se dépeuplent au profit du niveau fondamental. Enfin, dans le limite où
, c'est le début de condensation de Bose - Einstein: les niveaux excités se dépeuplent au profit du niveau fondamental. Enfin, dans le limite où
![]() K, tous les bosons se condensent sur le niveau fondamental. Cependant, il faut faire attention que ce terme de condensation est une image, car elle ne se produit non pas dans l'espace des positions, mais dans l'espace des impulsions. Ainsi, les bosons vont se condenser dans cet espace autour de la quantité de mouvement nulle, relativement à l'état fondamental.
K, tous les bosons se condensent sur le niveau fondamental. Cependant, il faut faire attention que ce terme de condensation est une image, car elle ne se produit non pas dans l'espace des positions, mais dans l'espace des impulsions. Ainsi, les bosons vont se condenser dans cet espace autour de la quantité de mouvement nulle, relativement à l'état fondamental.