Comportement à température nulle

Nous allons reprendre les calculs de $\mu$ ,

... à une température de

K. Des effets quantiques vont apparaître en relation avec le Principe de Pauli.

D'après (7.4), l'évolution du facteur de Fermi en fonction de l'énergie devient très simple: on peut la modéliser par un échelon de Heaviside ayant pour valeur 1 pour $0 \le \varepsilon \le \mu(0)$ , et 0 pour $\varepsilon > \mu(0)$ , où $\mu(0)$ désigne le potentiel chimique du système à température nulle. Nous avons donc:

$\displaystyle \left. N \right.$	$\displaystyle =$	$\displaystyle AV\int_{0}^{\infty}{d\varepsilon\sqrt{\varepsilon}\frac{1}{e^{\beta (\varepsilon - \mu)} + 1}}$
$\displaystyle \left. N \right.$	$\displaystyle =$	$\displaystyle AV\int_{0}^{\mu(0)}{d\varepsilon\sqrt{\varepsilon}}$

$\displaystyle \mu(0) = \frac{\hbar^{2}}{2m}\left(\frac{6\pi^{2}}{2s + 1}n\right)^{\frac{2}{3}}$

(7.11)

$\displaystyle \left. E \right.$	$\displaystyle =$	$\displaystyle AV\int_{0}^{\infty}{\frac{\varepsilon^{\frac{3}{2}}d\varepsilon}{e^{\beta (\varepsilon - \mu)} + 1}}$
$\displaystyle \left. E \right.$	$\displaystyle =$	$\displaystyle AV\int_{0}^{\mu(0)}{\varepsilon^{\frac{3}{2}}d\varepsilon}$
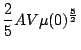$\displaystyle \left. E \right.$	$\displaystyle =$	$\displaystyle \frac{2}{5}AV\mu(0)^{\frac{5}{2}}$

L'énergie moyenne d'un fermion est donc $\frac{3}{5}\mu(0)$ . On introduit ici la température de Fermi du système par

Application numérique: Pour le cuivre, on obtient $\mu(0) \approx 7~$ eV, ce qui correspond à une énergie très élevée par rapport au produit $k_{B}T$ à température usuelle ( $\approx 300~$ K), de l'ordre de

eV.

L'énergie des électrons à température nulle est donc considérable, à cause du principe de Pauli. Ce cas de figure n'a donc rien à voir avec un raisonnement classique, lequel prévoit (cf. Drude) une énergie nulle à température nulle. Pour s'en convaincre, demandons-nous quelle température il faudrait attribuer à une particule classique pour qu'elle ait la même énergie moyenne qu'un électron à 0K. Pour cela, on écrit que $\overline{E}_{cl}(T) = \frac{3}{2}k_{B}T$ d'après le théorème d'équipartition de l'énergie, et d'autre part $\overline{E}_{cl}(T) = \frac{3}{5}k_{B}T_{F}$ pour répondre au problème. Il vient donc:

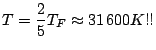
Il faut donc communiquer au gaz d'électrons une énergie colossale pour permettre l'occupation de chaque niveau d'énergie par une seule paire d'électrons de spin opposé.

Dans l'espace des vecteurs d'onde, on représente tous les états occupés par les fermions à l'intérieur d'une sphère, la sphère de Fermi. Son rayon, appelé norme du vecteur d'onde de Fermi, est donné par la relation: $\mu(0) = \frac{\hbar^{2}k_{F}^{2}}{2m}$ , soit:

Cette modélisation est intéressante car elle permet de représenter le système complètement dégénéré qu'est le gaz de Fermi. Les états qu'occupent les fermions correpondent aux sommets des parallélépipèdes engendrant la sphère de Fermi: ils sont disposés de l'état le plus bas à l'état le plus haut en respectant le principe de Pauli. Remarquant qu'il y a beaucoup plus de fermions à la périphérie de la sphère qu'en son centre, on en déduit logiquement que l'énergie moyenne du gaz de fermions est proche de l'énergie maximale des fermions se situant sur la sphère de Fermi, peuplant ce qu'on appelle le niveau de Fermi.

On définit alors l'énergie de Fermi comme étant l'énergie individuelle maximale d'un fermion dans l'état fondamental du système. Il s'agit en somme de l'énergie des fermions situés sur le niveau de Fermi. En terme d'occupation des niveaux, cela signifie que tous les niveaux d'énergie inférieure à $\varepsilon_{F}$ sont peuplés tandis que tous ceux ayant une énergie strictement supérieure à $\varepsilon_{F}$ sont vides. Forts de cette remarque, nous concluons que: