Comportement à $T \ll T_{F}$

Méthode de développement de Sommerfeld

On remarque tout d'abord que la structure des objets mathématiques manipulés est de la forme:

$$g(T,\mu) = \int_{0}^{\infty}{\overline{N}^{F}(\varepsilon,T,\mu)f(\varepsilon)d\varepsilon}$$

Par exemple, $f(\varepsilon) = \sqrt{\varepsilon}$ pour N, $f(\varepsilon) = \varepsilon^{\frac{3}{2}}$ pour E ...

Attention, la méthode de Sommerfeld est une méthode quantitative, mathématique, sans grand réalisme physique: nous allons ainsi supposer que toutes les grandeurs intervenant ici ($T$, $\mu$ ...) sont indépendantes entre elles.

Soit donc:

$$\left. g(0,\mu) \right. = \int_{0}^{\infty}{\overline{N}^{F}(\varepsilon,0,\mu)f(\varepsilon)d\varepsilon}$$

$$= \int_{0}^{\mu}{f(\varepsilon)d\varepsilon}$$

La méthode de Sommerfeld consiste à évaluer la différence:

$$\left. \delta g(T,\mu) \right. = g(T,\mu) - g(0,\mu)$$

$$= \int_{0}^{\infty}{\underbrace{\left(\overline{N}^{F}(\varepsilon,... ...lon,0,\mu)\right)}_{\delta N^{F}(T,\varepsilon,\mu)}f(\varepsilon)d\varepsilon}$$

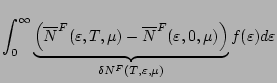Comme nous supposons que $T \ll T_{F}$, alors $\delta N^{F} \approx 0$ pour $\varepsilon$ très petit devant $\mu$: on peut donc étendre la borne inférieure de l'intégrale à $-\infty$. D'où:

$$\left. \delta g(T,\mu) \right. \approx \int_{-\infty}^{\mu}{\delta N^{F}f(\varepsilon)d\varepsilon} + \int_{\mu}^{\infty}{\delta N^{F}f(\varepsilon)d\varepsilon}$$

$$\approx \int_{-\infty}^{\mu}{\left(\frac{1}{e^{\beta(\varepsilon - \mu)} ... ...ft(\frac{1}{e^{\beta(\varepsilon - \mu)} + 1}\right)f(\varepsilon)d\varepsilon}$$

Posons le chagement de variable $x = \beta(\varepsilon - \mu)$:

$$\left. \delta g(T,\mu) \right. \approx k_{B}T\left[\int_{-\infty}^{0}{\left({\frac{1}{e^{x} + 1} - 1}\right)f(k_{B}Tx + \mu)dx} + \right.$$

$$\left. \int_{0}^{\infty}{\frac{1}{e^{x} + 1}f(k_{B}Tx + \mu)dx}\right]$$

$$\approx k_{B}T\left[-\int_{0}^{\infty}{\frac{1}{e^{x} + 1}f(\mu - k_{B}Tx)dx} + \right.$$

$$\left. \int_{0}^{\infty}{\frac{1}{e^{x} + 1}f(k_{B}Tx + \mu)dx}\right]$$

$$\approx k_{B}T\int_{0}^{\infty}{\frac{1}{e^{x} + 1}\left[f(\mu + k_{B}Tx) - f(\mu - k_{B}Tx)\right]dx}$$

Un développement limité à l'ordre 4 près de la quantité $f(\mu + k_{B}Tx) - f(\mu - k_{B}Tx)$ donne:

$$f(\mu + k_{B}Tx) - f(\mu - k_{B}Tx) \approx 2k_{B}Txf^{'}(\mu) + \frac{1}{3}(k_{B}Tx)^{3}f^{(3)}(\mu)$$

D'où:

$$\delta g(T,\mu) \approx k_{B}T\Big[2k_{B}Tf^{'}(\mu)\underbrace{\... ...{\int_{0}^{\infty}{\frac{x^{3}}{e^{x} + 1}dx}}_{=\ \ \frac{7\pi^{4}}{120}}\Big]$$

Finalement:

$$\fbox{$\displaystyle g(T,\mu) = g(0,\mu) + \frac{\pi^{2}}{6}(k_{B}T)^{2}f^{'}(\mu) +{\cal O}(T^4)$}$$ (7.14)

Appliquons le résultat précédent aux calculs de $\mu$, $E$ et $C_{V}$:

Calcul de $\mu(T)$

Nous avons:

$$\frac{N}{AV} = \int_{0}^{\infty}{N(\varepsilon,\mu,T)\sqrt{\varepsilon}d\varepsilon}$$

d'où :

$$\left. \frac{N}{AV} \right. = \int_{0}^{\mu(T)}{\sqrt{\varepsilon}d\varepsilon}\ + \ \frac{\pi^{2}}{6}(k_{B}T)^{2}\frac{1}{2\sqrt{\mu(T)}}$$

$$= \frac{2}{3}\mu(T)^{\frac{3}{2}} + \frac{\pi^{2}}{12}(k_{B}T)^{2}\frac{1}{\sqrt{\mu(T)}}$$

$$= \frac{2}{3}\mu(0)^{\frac{3}{2}} ~~~$$

Nous cherchons $\mu(T)$ sous la forme: $\mu(T) = \mu(0)\left(1 + aT^{2} +\cdots\right)$. Par conséquent, en se contentant de développements limités au second ordre en $\frac{T}{T_{F}}$, il vient:

$$\frac{2}{3}\mu(0)^{\frac{3}{2}} = \frac{2}{3}\mu(0)^{\frac{3}{2}}... ...2}] + \frac{\pi^{2}}{12}(k_{B}T)^{2}\mu(0)^{-\frac{1}{2}}[1 - \frac{a}{2}T^{2}]$$

soit:

$$0 = \frac{3a}{2} - \underbrace{\frac{a\pi^{2}}{16}\left(\frac{T}{T_{F}}\right)^{2}}_{\ll 1} + \frac{\pi^{2}}{8T_{F}^{2}}$$

d'où

$$a = -\frac{\pi^{2}}{12T_{F}^{2}}$$

et finalement:

$$\fbox{$\displaystyle \mu(T) = \mu(0)\left\{1 - \frac{\pi^{2}}{12}... ...{F}}\right)^{2} + {\cal O}\left[\left(\frac{T}{T_F}\right)^{4}\right]\right\}$}$$ (7.15)

$\mu(T)$ varie donc très peu par rapport à sa valeur à $0~$K.

Calcul de $E(T)$

De la même façon que précédemment, on a:

$$\frac{E}{AV} = \int_{0}^{\infty}{N(\varepsilon,\mu,T)\varepsilon^{\frac{3}{2}}d\varepsilon}$$

d'où d'après (7.14):

$$\left. \frac{E}{AV} \right. = \int_{0}^{\mu(T)}{\varepsilon^{\frac{3}{2}}d\varepsilon}\ + \ \frac{\pi^{2}}{6}(k_{B}T)^{2}\frac{3}{2}\sqrt{\mu(T)}$$

$$= \frac{2}{5}\mu(T)^{\frac{5}{2}} + \frac{\pi^{2}}{4}(k_{B}T)^{2}\sqrt{\mu(T)}$$

$$= \frac{2}{5}\mu(0)^{\frac{5}{2}}\left[1 - \frac{5\pi^{2}}{24}\left(\frac{T}{T_{F}}\right)^{2} + \cdots\right] +$$

$$\frac{\pi^{2}}{4}(k_{B}T)^{2}\sqrt{\mu(0)}\left[1 - \frac{\pi^{2}}{24}\left(\frac{T}{T_{F}}\right)^{2} + \cdots\right]$$

D'où:

$$\left. E(T) \right. = \frac{2}{5}AV\mu(0)^{\frac{5}{2}}\left[1 - \frac{5\pi^{2}}{24}\le... ...^{2} + \cdots\right] + \frac{\pi^{2}}{4}AV(k_{B}T)^{2}\mu(0)^{-2 + \frac{5}{2}}$$

$$= \frac{2}{5}AV\mu(0)^{\frac{5}{2}}\left[1 - \frac{5\pi^{2}}{24}\le... ...right)^{2} + \frac{5\pi^{2}}{8}\left(\frac{T}{T_{F}}\right)^{2} + \cdots\right]$$

$$= \frac{3}{5}N\mu(0)\left[1 + \frac{5\pi^{2}}{12}\left(\frac{T}{T_{F}}\right)^{2} + \cdots\right]$$

c'est-à-dire finalement:

$$\fbox{$\displaystyle E(T) = E(0)\left\{1 + \frac{5\pi^{2}}{12}\le... ...{F}}\right)^{2} + {\cal O}\left[\left(\frac{T}{T_F}\right)^{4}\right]\right\}$}$$ (7.16)

où $$E(0) = \frac{3}{5}Nk_B T_F$$.

Calcul de $C_{V}(T)$

$$C_{V}(T) = \left(\frac{\partial E}{\partial T}\right)_V$$ donne l'expression de la capacité thermique à volume constant, à température très petite devant la température de Fermi:

$$\left. C_{V}(T) \right. = \frac{5\pi^2}{6}E(0)\frac{T}{T_F^2} + {\cal O}\left[\left(\frac{T}{T_F}\right)^{3}\right]$$

$$= \frac{5\pi^2}{6}\times \frac{3}{5}Nk_B T_F \times\frac{T}{T_F^2} ~+~ {\cal O}\left[\left(\frac{T}{T_F}\right)^{3}\right]$$

donc:

$$\fbox{$\displaystyle C_{V}(T) = \frac{\pi^{2}}{2}Nk_{B}\left(\frac{T}{T_{F}}\right) + {\cal O}\left[\left(\frac{T}{T_F}\right)^{3}\right]$}$$ (7.17)

On voit que $C_{V}$ dépend effectivement de la température puisque varie linéairement avec elle: $C_{V} = \gamma T$. C'est différent du cadre classique où, d'après le théorème d'équipartition de l'énergie, $E = \frac{3}{2}Nk_{B}T$ implique $C_{V} = \frac{3}{2}Nk_{B}$, indépendant de T.

Calcul de J(T)

On a déjà vu que $$J = -\frac{2}{3}E$$ donc:

$$\fbox{$\displaystyle J(T) = -\frac{2}{3}E(0)\left\{1 + \frac{5\pi... ...{F}}\right)^{2} + {\cal O}\left[\left(\frac{T}{T_F}\right)^{4}\right]\right\}$}$$ (7.18)

Calcul de S(T)

$$S = -\frac{\partial J}{\partial T}$$ d'où:

$$\left. S(T) \right. = -\frac{\partial}{\partial T}\left[-\frac{5\pi^2}{18}E(0)\left(\frac{T}{T_F}\right)^2 + {\cal O}\left[\left(\frac{T}{T_F}\right)^{4}\right]\right]$$

$$= \frac{5\pi^2}{9}\frac{E(0)}{T_F}\left(\frac{T}{T_F}\right) + {\cal O}\left[\left(\frac{T}{T_F}\right)^{3}\right]$$

D'où:

$$\fbox{$\displaystyle S(T) = \frac{\pi^{2}}{3}Nk_{B}\left(\frac{T}{T_{F}}\right) + {\cal O}\left[\left(\frac{T}{T_F}\right)^{3}\right]$}$$ (7.19)

Calcul de F(T)

La limite thermodynamique étant atteinte, nous avons $$J = F - \mu N$$. Par conséquent:

$$\left. F(T) \right. = J(T) + N\mu(T)$$

$$= -\frac{2}{3}E(0)\left\{1 + \frac{5\pi^{2}}{12}\left(\frac{T}{T_{F}}\right)^{2} + {\cal O}\left[\left(\frac{T}{T_F}\right)^{4}\right]\right\} +$$

$$\frac{5}{3}E(0)\left\{1 - \frac{\pi^2}{12}\left(\frac{T}{T_F}\right)^2 + {\cal O}\left[\left(\frac{T}{T_F}\right)^{4}\right]\right\}$$

$$= E(0)\left\{1 - \frac{5\pi^2}{18}\left(\frac{T}{T_F}\right)^2 - \f... ...{T}{T_F}\right)^2 + {\cal O}\left[\left(\frac{T}{T_F}\right)^{4}\right]\right\}$$

soit finalement:

$$\fbox{$\displaystyle F(T) = E(0)\left\{1 - \frac{5\pi^{2}}{12}\le... ...{F}}\right)^{2} + {\cal O}\left[\left(\frac{T}{T_F}\right)^{4}\right]\right\}$}$$ (7.20)

Calcul de p(T)

On a:

$$p = -\frac{J}{V} = \frac{2}{3}\frac{E}{V}$$

donc:

$$\fbox{$\displaystyle p(T) = \frac{2}{5}\frac{N}{V}\mu(0)\left\{1 ... ...{F}}\right)^{2} + {\cal O}\left[\left(\frac{T}{T_F}\right)^{4}\right]\right\}$}$$ (7.21)