Equations générales

L'approximation continue étant licite, nous devons en premier lieu calculer la densité d'état $\rho(E)$. Pour cela, on se place dans l'espace des phases; les électrons étant indépendants et non-relativistes, nous avons $p = \sqrt{2mE}$. Les microétats d'énergie inférieure ou égale à $E$ sont donc compris dans la sphère de centre l'origine et de rayon $p$. D'où, tenant compte des dégénérescences de spin, nous avons:

$$\phi(E) = (2s + 1)\frac{V}{h^{3}}\frac{4}{3}\pi(2mE)^{\frac{3}{2}}$$

où $s = \frac{1}{2}$ (fermions), donc:

$$\rho(E) = \frac{4\pi V}{h^{3}}(2m)^{\frac{3}{2}}\sqrt{E}$$

ce qu'on notera désormais sous la forme:

$$\rho(E) = AV\sqrt{E}$$ (7.5)

où

$$A = \frac{4\pi}{h^{3}}(2m)^{\frac{3}{2}}$$

Calcul de $\mu$

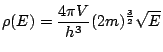
On applique (7.1):

$$\left. N \right. = \int_{0}^{\infty}{\rho(\varepsilon)d\varepsilon\frac{1}{e^{\beta (\varepsilon - \mu)} + 1}}$$

$$= AV\int_{0}^{\infty}{d\varepsilon\sqrt{\varepsilon}\frac{1}{e^{\beta (\varepsilon - \mu)} + 1}}$$

$$= AV(k_{B}T)^{\frac{3}{2}}\int_{0}^{\infty}{\frac{\sqrt{x}dx}{\frac{e^{x}}{\phi} + 1}}$$

où $x=\beta\varepsilon$ et $\phi = e^{\beta\mu}$ est la fugacité du système.

On reconnaît dans l'expression ci-dessus une intégrale de Fermi:

$$\fbox{$\displaystyle N = AV(k_{B}T)^{\frac{3}{2}}I_{\frac{1}{2}}(\phi)$}$$ (7.6)

Cette dernière relation est importante: c'est elle qui donne implicitement accès à $\mu$. Pour cela, on résout graphiquement l'équation:

$$\frac{N}{AV(k_{B}T)^{\frac{3}{2}}} = I_{\frac{1}{2}}(\phi)$$

Calcul de E

L'énergie du système est donnée par (7.2), un calcul identique à ce qui précède donne facilement:

$$\fbox{$\displaystyle E = AV(k_{B}T)^{\frac{5}{2}}I_{\frac{3}{2}}(\phi)$}$$ (7.7)

Remarque: On définit de façon générale les intégrales de Fermi par:

$$I_{\nu}(\phi) = \int_{0}^{\infty}{\frac{x^{\nu}dx}{\frac{e^{x}}{\phi} + 1}}$$

Calcul de J

Le grand potentiel du système est donné par (7.3); en remplaçant là encore $\rho(\varepsilon)$ par son expression (7.5), il vient:

$$J = -k_{B}TAV\int_{0}^{\infty}{\ln\left(1 + e^{-\beta(\varepsilon - \mu)}\right)\sqrt{\varepsilon}d\varepsilon}$$

ce qu'on intègre par parties:

$$J = -k_{B}TAV\left(\left[\frac{2}{3}\varepsilon^{\frac{3}{2}}\ln(... ...varepsilon^{\frac{3}{2}}d\varepsilon}{e^{\beta(\varepsilon - \mu)} + 1}}\right)$$

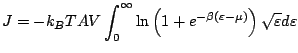
Le terme tout intégré est nul par croissances comparées et il s'ensuit:

$$\fbox{$\displaystyle J = -\frac{2}{3}E$}\index{Potentiel!grand}$$ (7.8)

On peut alors en déduire les valeurs de $S$, $F$ et $p$ par les relations énoncées en fin de premier paragraphe.