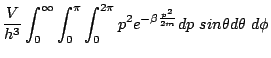Etude de la translation

suivant: Propriétés énergétiques monter: Gaz parfaits monoatomiques précédent: Gel des degrés de Table des matières Index

Etude de la translation

Cherchons l'expression de la fonction de partition de translation:

$\displaystyle \left. z_{\text{tr}} \right.$	$\displaystyle =$	$\displaystyle \frac{1}{h^3}\times \int\int d^3q ~d^3p ~e^{-\beta\frac{p^2}{2m}}$
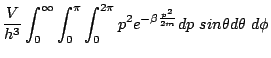	$\displaystyle =$	$\displaystyle \frac{V}{h^3} \int_{0}^{\infty}\int_{0}^{\pi}\int_{0}^{2\pi}{p^2 e^{-\beta\frac{p^2}{2m}} dp~sin\theta d\theta ~d\phi}$
	$\displaystyle =$	$\displaystyle \frac{4\pi V}{h^3} \int_{0}^{\infty}{-2m\frac{\partial e^{-\beta\frac{p^2}{2m}}}{\partial \beta}dp}$
	$\displaystyle =$	$\displaystyle -\frac{8\pi mV}{h^3} \frac{\partial}{\partial\beta} \int_{0}^{\infty}{e^{-\beta\frac{p^2}{2m}}dp}$
	$\displaystyle =$	$\displaystyle -\frac{4\pi mV}{h^3}\sqrt{2\pi m} ~\frac{\partial}{\partial\beta}\left(\frac{1}{\sqrt{\beta}}\right)$
	$\displaystyle =$	$\displaystyle \frac{V}{h^3}\times\left(\frac{2\pi m}{\beta}\right)^{\frac{3}{2}}$

D'où:

$\displaystyle z_{\text{tr}} = V \left(\frac{2\pi mk_{B}T}{h²}\right)^{\frac{3}{2}}$

(5.5)

La quantité:

$\displaystyle \fbox{$\displaystyle \Lambda~ = ~\frac{h}{\sqrt{2m\pi k_{B}T}}$}$

(5.6)

est donc homogène à une longueur et peut s'écrire, d'après la loi de De Broglie, comme le quotient de la constante de Planck par une impulsion . Cette dernière s'écrivant $p = \sqrt{2m\varepsilon_{\text{tr}}}$ , $\Lambda$ apparaît comme la longueur d'onde thermique de De Broglie que l'on peut associer à une particule d'énergie $\pi k_{B}T$ .

Nous avons ainsi:

$\displaystyle z_{\text{tr}} = \frac{V}{\Lambda^{3}}$

(5.7)

Conclusion:

La fonction de partition totale d'une particule s'écrit finalement:

$\displaystyle \fbox{ $\displaystyle z = g_{0}^{\text{el}} \frac{V}{\Lambda^{3}}$}$

(5.8)

Dans son expression, nous avons conservé $g_0^{\text{el}}$ mais pas $g_0^{\text{nucl}}$ , alors qu'il s'agit de deux constantes ne contribuant pas à la détermination des propriétés thermodynamiques du système (celles-ci faisant intervenir des dérivées du logarithme de la fonction de partition). Cela permet en effet de rappeller qu'il peut ne pas y avoir gel des degrés de liberté électronique, chose impossible avec les degrés de liberté nucléaires.

Revenons à l'approximation de Maxwell-Boltzmann : étant donné que ${g_{0}^{\text{el}}}$ est un entier naturel proche de l'unité, $z\gg N \Leftrightarrow z_{\text{tr}} \gg N$ , i.e. $\Lambda^{3} \ll \frac{V}{N} = d^{3}$ , où d représente la distance moyenne entre deux atomes du gaz. Il suffit donc d'avoir:

$\displaystyle {\bf\Lambda \ll d}$

(5.9)

Cette dernière inégalité est importante : non seulement elle indique le critère d'application de l'approximation de Maxwell-Boltzmann mais aussi la condition de validité de l'approximation classique.

suivant: Propriétés énergétiques monter: Gaz parfaits monoatomiques précédent: Gel des degrés de Table des matières Index

Clément Baruteau 2003-04-30