Particules identiques et discernables

suivant: Particules identiques et indiscernables monter: Systèmes de particules indépendantes précédent: Systèmes de particules indépendantes Table des matières Index

Particules identiques et discernables

Des particules sont qualifiées de discernables si elles occupent un site géographique précis, comme par exemple les ions d'un réseau cristallin, et si le libre parcours moyen d'une particule à partir de son site est très petit devant la distance moyenne entre deux sites consécutifs.

Chaque microétat $\phi_{\ell}$ du système des particules discernables peut s'écrire comme le produit des microétats individuels $\phi_{\lambda}$ de chaque particule:

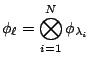
$\displaystyle \displaystyle \phi_{\ell} = \bigotimes_{i=1}^N \phi_{\lambda _i}$

de même que l'énergie $E_{\ell}$ correspondante à $\phi_{\ell}$ est la somme des énergies propres relatives aux différents états individuels:

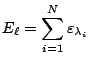
$\displaystyle E_{\ell} = \sum_{i=1}^N {\varepsilon_{\lambda _i}}$

En somme, l'hamiltonien du système des particules est à variables séparables; le calcul de la fonction de partition du système total est donc aisé dans la mesure où les différents états individuels sont indépendants les uns des autres:

$\displaystyle \left. Z \right.$	$\displaystyle =$	$\displaystyle \sum_{\ell=1}^{\infty}{e^{-\beta E_{\ell}}}$
	$\displaystyle =$	$\displaystyle \sum_{\lambda_1,...,\lambda_N}{e^{-\beta(\varepsilon_{\lambda_1} + \ldots + \varepsilon_{\lambda_N})}}$
	$\displaystyle =$	$\displaystyle \sum_{\lambda_1}{e^{-\beta\varepsilon_{\lambda_1}}} \times\ldots\times \sum_{\lambda_N}{e^{-\beta\varepsilon_{\lambda_N}}}$

D'où finalement:

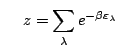$\displaystyle \fbox{$\displaystyle Z = z^N$}~~~~$ avec $\displaystyle ~~~~z = \sum_{\lambda}{e^{-\beta\varepsilon_{\lambda}}}$

(4.26)

étant la fonction de partition d'une particule donnée. De même:

$\displaystyle F$	=	$-k_B \ln Z$	=	$-Nk_B \ln z$	i.e.	$\displaystyle F$	=
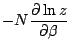$\displaystyle \overline{E}$	=	$\displaystyle -\frac{\partial \ln Z}{\partial \beta}$	=	$\displaystyle -N\frac{\partial \ln z}{\partial \beta}$	donc	$\displaystyle \overline{E}$	=	$N\overline{\varepsilon}$
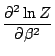$\displaystyle {\Delta E}^2$	=	$\displaystyle \frac{\partial^2 \ln Z}{\partial \beta^2}$	=	$\displaystyle N\frac{\partial^2 \ln z}{\partial \beta^2}$	donc	$\displaystyle \Delta E$	=	$\sqrt{N} \Delta\varepsilon$

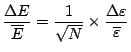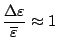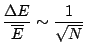On remarquera que $\displaystyle \frac{\Delta E}{\overline{E}} = \frac{1}{\sqrt{N}}\times\frac{\Delta\varepsilon}{\overline{\varepsilon}}$ . Or pour une particule donnée, la dispersion de l'énergie est assez importante - cf. (5.11) - et typiquement $\displaystyle \frac{\Delta\varepsilon}{\overline{\varepsilon}} \approx 1$ si bien que: $\displaystyle \frac{\Delta E}{\overline{E}} \sim \frac{1}{\sqrt{N}}$ .

suivant: Particules identiques et indiscernables monter: Systèmes de particules indépendantes précédent: Systèmes de particules indépendantes Table des matières Index

Clément Baruteau 2003-04-30