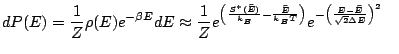 d'après (4.12)
d'après (4.12)
Maintenant que nous avons introduit l'énergie libre d'un système, nous allons vérifier que les différentes grandeurs thermodynamiques des descriptions microcanonique et canonique sont équivalentes à la limite thermodynamique. Nous avons vu précédemment que:
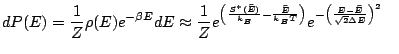 d'après (4.12)
d'après (4.12)
D'où:
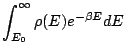 |
|||
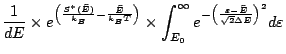 |
La gausienne étant relativement piquée sur
![]() , on peut considérer que la borne inférieure de l'intégrale est
, on peut considérer que la borne inférieure de l'intégrale est ![]() , ainsi:
, ainsi:
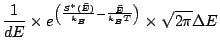 |
|||
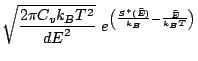 |
Donc:
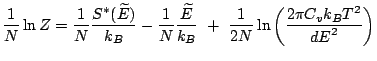
La méthode est classique: pour ne conserver que les termes prépondérants à la limite thermodynamique, il suffit de prendre la limite quand ![]() tend vers
tend vers ![]() de l'expression précédente. Or:
de l'expression précédente. Or:
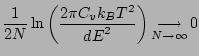 .
.
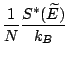 et
et
D'où, en passant à la limite quand
![]() :
:
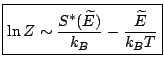 |
(4.24) |
| (4.25) |
On avait déjà établi en 4.2.2 l'équivalence entre les énergie microcanonique et canonique pour un système macroscopique à la limite thermodynamique. Nous voyons à présent qu'il en est de même pour l'énergie libre et l'entropie. On généralise sans problème le procédé aux autres grandeurs thermodynamiques, ce qu'on explicite dans le tableau 4.1, page ![]() .
.
|