Généralisation à l'échange de volume et de particules

Nous devons en premier lieu donner les définitions suivantes:

Définition: On définit la pression microcanonique $p^*$ par:

$$\fbox{$\displaystyle \frac{p^*}{T^*} = \left(\frac{\partial S^*}{\partial V}\right)$}$$ (3.17)

Définition: On définit le potentiel chimique microcanonique $\mu^*$ par:

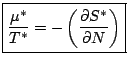$$\fbox{$\displaystyle \frac{\mu^*}{T^*} = -\left(\frac{\partial S^*}{\partial N}\right)$}$$ (3.18)

Afin de généraliser le travail précédent, il suffit de considérer que la paroi séparant les deux sous-systèmes $s_1$ et $s_2$ est, en plus d'être diatherme, mobile et poreuse. Une démarche identique à celle menée au paragraphe précédent aboutit au fait que l'état d'équilibre final correspond à:

-

un équilibre thermique: ${T_1}^* = {T_2}^*$.

-

un équilibre mécanique: ${p_1}^* = {p_2}^*$.

-

un équilibre osmotique: ${\mu_1}^* = {\mu_2}^*$.

Globalement: notons $y$ une variable interne quelconque (volume, nombre de particules...) d'un système isolé. Soit $P$ la propriété ``appartenir à l'intervalle $[y,y+dy]$'' et soit $\varpi (E,x;y)dy$ le nombre de microétats vérifiant $P$ (on parle de microétats favorables). On note $\Omega(E,x)$ le nombre total de microétats accessibles au système. La probabilité pour que la propriété $P$ soit réalisée est le quotient du nombre de microétats favorables à $P$ par le nombre total de microétats, c'est-à-dire:

$$\omega(E,x;y)dy = \frac{\varpi(E,x;y)dy}{\Omega(E,x)}$$

La distribution de probabilité $\omega(E,x;y) \equiv \omega(y)$ est, pour un système macroscopique, une gaussienne centrée sur sa valeur la plus probable $\widetilde{y}$ et d'écart type $\sigma$ vérifiant $$\frac{\sigma}{\widetilde{y}} \propto \frac{1}{\sqrt{N}}$$:

$$\omega(y) \approx \omega(\widetilde{y})e^{-\frac{(y-\widetilde{y})^2}{2\sigma^2}}$$

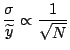Toutefois, cette distribution peut en pratique être considérée comme un pic de Dirac centré sur $\widetilde{y}$.