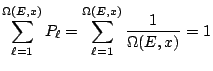Principe fondamental

Le principe fondamental énonce que tous les microétats accessibles à un système en situation microcanonique sont équiprobables.

En admettant ce postulat, la distribution microcanonique des microétats est la suivante: la probabilité d'occupation, par le système isolé en équilibre, du microétat $\phi_l$ d'énergie $E_{\ell}$ est:

$$\fbox{$\displaystyle P_{\ell} = \left\{ \begin{array}{ll} \frac{1... ...xt{ si $E \leq E_{\ell} \leq E+dE$} \\ 0 & \text{ sinon } \end{array} \right.$}$$ (3.2)

Tous les microétats sont ainsi équiprobables. Cette distribution est bien normalisée dans la mesure où:

$$\sum_{\ell = 1} ^{\Omega(E,x)} {P_{\ell}} = \sum_{\ell = 1} ^{\Omega(E,x)} {\frac{1}{\Omega(E,x)}} = 1$$