Il s'agit du cas limite de la distribution binomiale où ![]() et
et ![]() . Dans ces conditions:
. Dans ces conditions:
 et
et

Ainsi,
 . Posons
. Posons
![]() :
:
 |
(2.20) |
Remarquons que cette distribution est bien normalisée à 1 car:

Valeur moyenne de la distribution:
 |
|||
 |
|||
 |
Etant donné que ![]() , nous avons finalement:
, nous avons finalement:
| (2.21) |
La valeur moyenne de la distribution poissonienne est donc égale à la valeur moyenne de la distribution binomiale.
Variance de la distribution:
Comme pour la distribution binomiale, il nous faut d'abord calculer
[4]![]() :
:
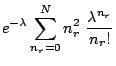 |
|||
 |
|||
 |
|||
 |
|||
 car car |
Finalement, la variance de la distribution de Poisson est:
| (2.22) |
Là encore, l'amplitude relative des fluctuations de ![]() autour de sa valeur moyenne vérifie:
autour de sa valeur moyenne vérifie:
