Distribution binomiale

La distribution binomiale est très classique en physique statistique, par ses applications dans les phénomènes de marche au hasard. De façon très générale, nous considérons un événement quelconque dont la probabilité de réalisation est $p$ et celle de non-réalisation $q$. Nous avons bien entendu $p+q =1$.
[4]Nous effectuons $N$ mesures de cet événement et cherchons la probabilité $P(n)$ d'obtenir $n$ réalisations parmi $N$:

$$P(n) = {\rm C}_N^n ~p^n ~q^{N-n} ~=~ \frac{N!}{n! ~(N-n)!} ~p^n ~q^{N-n}$$ (2.17)

Remarquons que: $$\sum_{n=0}^N {P(n)} = \sum_{n=0}^N {{\rm C}_N^n ~p^n ~q^{N-n}} = \left(p+q\right)^N = 1$$.

Valeur moyenne de la distribution:

Notons à présent $n_r$ le nombre de réalisations et $n_{\overline{r}}$ son complémentaire ( $n_r + n_{\overline{r}} = N$); calculons $<n_r>$:

$$<n_r> ~= \sum_{{n_r}=0}^N {n_r ~{\rm C}_N^{n_r} ~p^{n_r} ~q^{N-{n_r}}}$$

L'astuce consiste à assimiler $p$ et $q$ à des variables indépendantes et continues, de sorte que $$n_r ~p^{n_r} = p\times\frac{\partial p^{n_r}}{\partial p}$$. D'où:

$$\left. <n_r> \right. =~ \sum_{{n_r} = 0}^N {\rm C}_N^{n_r} \left(p\frac{\partial p^{n_r}}{\partial p}\right) ~q^{N - n_r}$$

$$= p\frac{\partial}{\partial p}\sum_{{n_r}=0}^N {{\rm C}_N^{n_r} ~p^{n_r} ~q^{N-{n_r}}}$$

$$= p\frac{\partial}{\partial p}\left(p+q\right)^N$$

$$= Np\left(p+q\right)^{N-1}$$

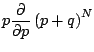Finalement, le nombre moyen de réalisations de notre événement sur un total de $N$ mesures est:

$$\fbox{$\displaystyle <n_r> ~= Np$}$$ (2.18)

un résultat somme toute cohérent.

De même, étant donné que $$<n_r> + <n_{\overline{r}}>~ = N$$, on a $$<n_{\overline{r}}>~ = N(1 - p) = Nq$$.

Variance de la distribution:

La variance ${\sigma_{n_r}}^2$ de la distribution est définie par $${\sigma_{n_r}}^2 = ~<\left(n_r - <n_r>\right)^2>~$$ i.e.

$${\sigma_{n_r}}^2 =~ <n_r^2>~ - <n_r>^2$$

Or $$<n_r^2>~ = \sum_{{n_r}=0}^N {n_r^2 ~{\rm C}_N^{n_r} ~p^{n_r} ~q^{N-{n_r}}}$$. Comme précédemment, on utilise l'astuce suivante: si $p$ et $q$ sont des variables indépendantes et continues, nous avons: $$n_r^2 ~p^{n_r} = n_r \times p\frac{\partial p^{n_r}}{\partial p} = \left(p\frac{\partial}{\partial p}\right)^2 p^{n_r}$$. Ainsi,

$$\left. <n_r^2> \right. = \left(p\frac{\partial}{\partial p}\right)^2 \sum_{{n_r}=0}^N {{\rm C}_N^{n_r} ~p^{n_r} ~q^{N-{n_r}}}$$

$$= \left(p\frac{\partial}{\partial p}\right)^2 \left(p+q\right)^N$$

$$= p\frac{\partial}{\partial p}\left[Np (p+q)^{N-1}\right]$$

$$= Np\left\{(p+q)^{N-1} + p(N-1)(p+q)^{N-2}\right\}$$

$$= Np\left(1 + (N-1)p\right) = Np\left(Np + q\right)$$

$$= \underbrace{N^2 p^2}_{<n_r>^2} + Npq$$

Donc:

$$\fbox{$\displaystyle {\sigma_{n_r}}^2 =~ <n_r^2>~ - <n_r>^2 ~= Npq$}$$ (2.19)

L'amplitude relative des fluctuations de $n_r$ autour de sa valeur de moyenne est alors:

$$\displaystyle \frac{\sigma_{n_r}}{<n_r>} = \frac{\sqrt{Npq}}{Np} \propto \frac{1}{\sqrt{N}}$$