Pour décrire un système macroscopique, nous avons jusqu'à maintenant adopté une approche temporelle, consistant à effectuer un très grand nombre de mesures sur le système. Soit une grandeur physique notée ![]() dont les différentes valeurs possibles sont indexées par
dont les différentes valeurs possibles sont indexées par ![]() . Avec cette démarche, nous pouvons écrire que la valeur moyenne temporelle de
. Avec cette démarche, nous pouvons écrire que la valeur moyenne temporelle de ![]() ,
,
![]() , est égale à:
, est égale à:

 et, comme précédemment,
et, comme précédemment,
L'approche du thermodynamicien Gibbs est différente: au lieu de prendre un unique système sur lequel on effectue un très grand nombre de mesures, on prend au contraire un très grand nombre de systèmes - ![]() - dont on effectue la mesure à un instant donné. On réalise dans ce cas une moyenne d'ensemble. Calculons justement la moyenne d'ensemble de notre grandeur
- dont on effectue la mesure à un instant donné. On réalise dans ce cas une moyenne d'ensemble. Calculons justement la moyenne d'ensemble de notre grandeur ![]() :
:
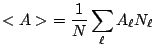
Or on a vu que pour ![]() assez grand,
assez grand,
 . D'où pour
. D'où pour ![]() assez grand, nous avons:
assez grand, nous avons:
 |
(2.15) |
Il s'agit du principe ergodique: on postule que moyenne temporelle et moyenne d'ensemble sont équivalentes. Néanmoins, une moyenne temporelle est plus pratique dans la mesure où elle ne fait intervenir qu'un seul système d'étude, contrairement à la moyenne d'ensemble qui en fait intervenir un nombre indéterminé.