Au lieu d'étudier directement le nombre de microétats ![]() , nous en étudions le logarithme népérien:
, nous en étudions le logarithme népérien:
Cette dernière relation nous permet de déterminer la valeur la plus probable de ![]() ,
,
![]() , définie par la relation
, définie par la relation
 . Or:
. Or:
 |
![$\displaystyle -\frac{N}{2}\left[\frac{1}{N}\ln\left(1 + \frac{\widetilde{m}}{N}...
...} - \frac{1}{N}\ln\left(1 - \frac{\widetilde{m}}{N}\right) - \frac{1}{N}\right]$](img331.png) |
||
 |
D'où

La valeur la plus probable de ![]() est nulle, ce qui signifie que les valeurs les plus probables pour
est nulle, ce qui signifie que les valeurs les plus probables pour ![]() et
et ![]() sont précisément égales à
sont précisément égales à
![]() , ce que nous avions intuitivement prédit.
, ce que nous avions intuitivement prédit.
Nous pouvons alors approcher la distribution des microétats ![]() . Pour cela, on remarque que
. Pour cela, on remarque que
![]() pour effectuer les développements limités:
pour effectuer les développements limités:
 .
.
 |
|||
![$\displaystyle \left. \left(1 - \frac{m}{N}\right)\left(-\frac{m}{N} - \frac{m^2}{2N^2}\right)\right]$](img340.png) |
|||
 |
Posons
![]() , le nombre de microétats nécessaires à la réalisation du macroétat ``
, le nombre de microétats nécessaires à la réalisation du macroétat ``![]() '' est:
'' est:
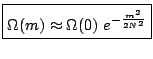 |
(2.4) |
 |
(2.5) |
On remarque que la distribution des microétats recherchée est approximativement une gaussienne alors qu'a priori elle n'était que binomiale: on vient d'illustrer le théorème de la limite centrale. Cette gaussienne est centrée sur l'origine et a pour écart quadratique moyen
![]() . Cette approximation n'est licite qu'à condition que
. Cette approximation n'est licite qu'à condition que ![]() soit suffisamment grand, c'était la condition d'exploitation de l'approximation de Stirling. En pratique, il suffit que
soit suffisamment grand, c'était la condition d'exploitation de l'approximation de Stirling. En pratique, il suffit que
![]() pour pouvoir exploiter l'approximation gaussienne.
pour pouvoir exploiter l'approximation gaussienne.
De l'étude précédente, il résulte donc que
![]() donc:
donc:

Intéressons-nous de plus près à l'amplitude relative des fluctuations de ![]() et
et ![]() autour de leur valeur la plus probable: celle-ci est égale à
autour de leur valeur la plus probable: celle-ci est égale à
[4]
 . Or
. Or ![]() est de l'ordre de grandeur du nombre d'Avogadro, si bien que
est de l'ordre de grandeur du nombre d'Avogadro, si bien que
![]() ! L'amplitude des fluctuations de
! L'amplitude des fluctuations de ![]() et
et ![]() est donc négligeable devant leur valeur finale.
est donc négligeable devant leur valeur finale.
Conclusions:
Remarque: La distribution gaussienne des microétats est si étroite qu'elle est assimilée en pratique à un pic de Dirac centré sur sa valeur la plus probable - qui est aussi sa valeur moyenne -.