Théorie des chaleurs molaires

Dans le cas des gaz parfaits monoatomiques: $\forall T$, $U = \frac{3}{2}RT$ et $H = \frac{5}{2}RT$. Donc $\gamma = \frac{5}{3}$.

Dans le cas des gaz parfaits diatomiques, les degrés de liberté internes interviennent différemment selon la température:

a)

pour T < 30 K: seuls les trois degrés de liberté de translation sont à considérer: $U = \frac{3}{2}RT$ et de nouveau $\gamma = \frac{5}{3}$.

b)

pour 300 K < T < 2000 K (cas usuel): on a trois degrés de liberté de translation et deux degrés de liberté de rotation supplémentaires; d'après le théorème d'équipartition de l'énergie: $U = \frac{5}{2}RT$ et $H = \frac{7}{2}RT$. Donc $\gamma = \frac{7}{5}$.

c)

pour T > 2000 K: la molécule peut vibrer autour de son barycentre, mais la contribution énergétique de cette vibration est ``double'' (en 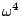$\omega^{4}$ dans l'hamiltonien). Mais Les degrés de liberté de rotation s'avérant être négligeables devant ceux de rotation, il s'agit en somme du même cas que précédemment: $\gamma = \frac{7}{5}$

d)

pour T > 6000 K: on doit prendre en compte trois degrés de liberté de translation, les deux degrés de liberté de rotation ainsi que le degré de liberté de vibration (qui compte ``double''), ce qui donne en tout $U = \frac{7}{2}RT$ et $H = \frac{9}{2}RT$ et ainsi $\gamma = \frac{9}{7}$.