




suivant: Applications du premier principe
monter: Premier principe de la
précédent: Premier principe
Table des matières
Index
Par la suite, nous ne considérons que le travail des forces de pression. Soit donc un système constitué d'un fluide séparé de l'extérieur par un piston qui se déplace selon l'axe (O ), et soumis à la force extérieure
), et soumis à la force extérieure
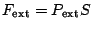 . Le travail élémentaire exercé par cette force est:
. Le travail élémentaire exercé par cette force est:
où
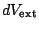 est l'accroissement différentiel de volume pour le milieu extérieur, donc opposé au petit élément de volume perdu par le système. D'où:
est l'accroissement différentiel de volume pour le milieu extérieur, donc opposé au petit élément de volume perdu par le système. D'où:
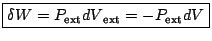 |
(1.11) |
Rappelons encore que 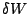 est une grandeur algébrique:
est une grandeur algébrique:
- -
- si
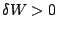 : le système reçoit effectivement du travail, i.e.
: le système reçoit effectivement du travail, i.e. 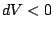 et
et
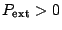 (le système subit une compression).
(le système subit une compression).
- -
- si
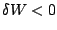 : le système fournit effectivement du travail au milieu extérieur, i.e.
: le système fournit effectivement du travail au milieu extérieur, i.e. 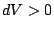 et
et
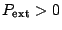 (le système subit une détente).
(le système subit une détente).
De plus, dans le cas d'une transformation quasi-statique ou même réversible, on a, à chaque instant,
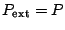 , si bien que
, si bien que
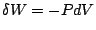 . On peut dans ce cas représenter graphiquement le travail des forces pressantes dans le diagramme
. On peut dans ce cas représenter graphiquement le travail des forces pressantes dans le diagramme 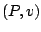 de Clapeyron. Il existe deux situations:
de Clapeyron. Il existe deux situations:
- -
- cas des transformations ouvertes: le travail
 est alors égal à l'opposé de l'aire algébrique comprise sous la courbe du diagramme de Clapeyron (cf. figure (1.1), page
est alors égal à l'opposé de l'aire algébrique comprise sous la courbe du diagramme de Clapeyron (cf. figure (1.1), page ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
).
Figure 1.1:
Diagramme de Clapeyron: cas d'une transformation ouverte.
|
|
- -
- cas des transformations cycliques:
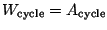 . Si
. Si
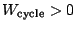 , le cycle est récepteur et est parcouru dans le sens trigonométrique, sinon (
, le cycle est récepteur et est parcouru dans le sens trigonométrique, sinon (
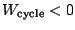 ) le cycle est moteur et est parcouru dans le sens horaire (cf. figure (1.2), page
) le cycle est moteur et est parcouru dans le sens horaire (cf. figure (1.2), page ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
).
Figure 1.2:
Diagramme de Clapeyron: cas d'une transformation cyclique. Ici, le cycle est parcouru dans le sens trigonométrique: il s'agit d'un cycle récepteur.
|
|





suivant: Applications du premier principe
monter: Premier principe de la
précédent: Premier principe
Table des matières
Index
Clément Baruteau
2003-04-30
![]() ), et soumis à la force extérieure
), et soumis à la force extérieure
![]() . Le travail élémentaire exercé par cette force est:
. Le travail élémentaire exercé par cette force est:
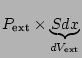
![]() est une grandeur algébrique:
est une grandeur algébrique:
![]() , si bien que
, si bien que
![]() . On peut dans ce cas représenter graphiquement le travail des forces pressantes dans le diagramme
. On peut dans ce cas représenter graphiquement le travail des forces pressantes dans le diagramme ![]() de Clapeyron. Il existe deux situations:
de Clapeyron. Il existe deux situations: