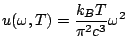Loi de Planck

suivant: Loi de Stefan-Boltzmann monter: Les lois du rayonnement précédent: Les lois du rayonnement Table des matières Index

Loi de Planck

Le corps noir ayant un volume macroscopique, nous faisons l'hypothèse que le nombre de photons y est suffisamment élevé pour effectuer l'approximation continue. Ainsi, le nombre de photons d'énergie comprise entre $\varepsilon$ et $\varepsilon+d\varepsilon$ est :

$\displaystyle N = \rho(\varepsilon)d\varepsilon\frac{1}{e^{\beta \varepsilon}-1}$

et l'énergie totale du rayonnement électromagnétique dans cet intervalle est:

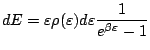
$\displaystyle dE = \varepsilon\rho(\varepsilon)d\varepsilon\frac{1}{e^{\beta \varepsilon}-1}$

Or $\rho(\varepsilon)d\varepsilon$ = $\rho(\omega)d\omega$ , d'où à partir de $\varepsilon = \hbar\omega$ et de (9.1), il vient:

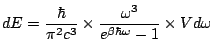
$\displaystyle dE = \frac{\hbar}{\pi^{2}c^{3}}\times\frac{\omega^{3}}{e^{\beta\hbar\omega} - 1}\times Vd\omega$

ce qu'on écrit sous la forme $d E = V u(\omega, T)d\omega$ où $u(\omega,T)$ est la densité spectrale par unité de volume, c'est elle que l'on mesure expérimentalement. C'est son expression que donne la loi de Planck:

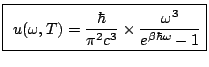$\displaystyle \fbox{ $\displaystyle u(\omega,T) = \frac{\hbar}{\pi^{2}c^{3}}\times\frac{\omega^{3}}{e^{\beta\hbar\omega} - 1}$}$

(9.8)

Il est intéressant d'étudier asymptotiquement cette loi de Planck:

*

à faible fréquence: on a $\hbar\omega \ll k_{B}T$ donc $e^{\beta\hbar\omega} - 1 \approx \beta\hbar\omega$ . Finalement:

$\displaystyle u(\omega,T) \approx \frac{k_{B}T}{\pi^{2}c^{3}}\omega^{2}$

(9.9)

c'est la loi de Rayleigh-Jeans.

*

à haute fréquence: on a $\hbar\omega \gg k_{B}T$ donc $e^{\beta\hbar\omega} - 1 \approx e^{\beta\hbar\omega}$ et finalement

$\displaystyle u(\omega,T) \approx \frac{\hbar}{\pi^{2}c^{3}}\omega^{3}e^{-\beta\hbar\omega}$

(9.10)

c'est la loi de Wien.

Nous allons maintenant calculer l'abscisse du maximum de la courbe $u(\omega,T) = f(\omega)$ . Pour cela, nous avons à résoudre l'équation suivante:

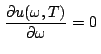$\displaystyle \left. \frac{\partial u(\omega,T)}{\partial\omega} = 0 \right.$	$\displaystyle \Rightarrow$	$\displaystyle \frac{\hbar}{\pi^{2}c^{3}}\left[\frac{3\omega^{2}(e^{\beta\hbar\o... ...\hbar\omega^{3}e^{\beta\hbar\omega}}{(e^{\beta\hbar\omega} - 1)^{2}}\right] = 0$
	$\displaystyle \Rightarrow$	$\displaystyle 3(e^{\beta\hbar\omega} - 1) - \beta\hbar\omega e^{\beta\hbar\omega} = 0$
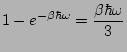	$\displaystyle \Rightarrow$	$\displaystyle 1 - e^{-\beta\hbar\omega} = \frac{\beta\hbar\omega}{3}$
	$\displaystyle \Rightarrow$	$\displaystyle 1 - e^{-x} = \frac{x}{3}$

où l'on a posé $x = \beta\hbar\omega$ . Cette équation se résout numériquement, on obtient $x \approx 2,821$ . On a ainsi accès à l'abscisse du maximum de la courbe de rayonnement du corps noir:

$\displaystyle \omega_{max} = 2,821\frac{k_{B}T}{\hbar}$

(9.11)

Il s'agit là de la loi de déplacement de Wien: plus la température augmente, plus l'abscisse du maximum de la courbe de rayonnement du corps noir augmente et est décalé vers les courtes longueurs d'onde.

Remarque: historiquement, le traitement du gaz de photons a été établi par l'association, à chaque mode propre du corps noir, d'un oscillateur harmonique classique et non quantique. Ainsi, le théorème d'équipartition de l'énergie implique une énergie égale à $k_{B}T$ pour chaque oscillateur, et la quantité calculée précédemment valait $dE = \rho(\omega)d\omega ~k_{B}T$ , c'est-à-dire

$\displaystyle dE = Vk_{B}T\frac{\omega^{2}}{\pi^{2}c^{3}}d\omega$

et la densité spectrale ainsi obtenue était:

$\displaystyle u(\omega,T) = \frac{k_{B}T}{\pi^{2}c^{3}}\omega^{2}$

ce qui n'est pas autre chose que la loi de Rayleigh-Jeans, mais valable pour toute gamme de fréquence... problématique car contraire aux résultats expérimentaux et diverge grossièrement de toute façon. C'est pour cela qu'il s'agit de l'une des premières expériences non expliquables en termes de mécanique ``classique''.

suivant: Loi de Stefan-Boltzmann monter: Les lois du rayonnement précédent: Les lois du rayonnement Table des matières Index

Clément Baruteau 2003-04-30