Etats quantiques individuels

Le champ électromagnétique le plus général dans la cavité peut s'écrire comme une superposition linéaire d'ondes planes monochromatiques, sous la forme $e^{i(\vec{k}.\vec{r} - \omega(k)t)}$ . Ainsi, chaque mode propre de la cavité, que nous noterons `` $\lambda$ '', est caractérisé par une valeur quantifiée du module du vecteur d'onde: $\vec{k_{\lambda}}$ . A un mode $\lambda$ donné va donc correspondre une unique relation de dispersion: $\omega_{\lambda} = k_{\lambda}c$ , les composantes $k_{\lambda}$ du vecteur d'onde étant données par les conditions limites périodiques (voir chapitre 2): $\displaystyle k_{\lambda} = n_{\lambda}\frac{2\pi}{L_{\alpha}}$ , où $n_{\lambda}$ est un entier relatif.

Comme nous faisons l'hypothèse de la propagation d'ondes électromagnétiques planes i.e. transverses, chaque mode propre possède deux directions de polarisation, qui sont les deux directions orthogonales à celle du vecteur d'onde correspondant.

Calculons à présent la densité spectrale des modes propres: pour cela, on se place dans l'espace des vecteurs d'onde et nous cherchons combien de modes propres ont un vecteur d'onde dont la norme est comprise entre

fixé. Le raisonnement est classique: le volume accessible dans l'espace des $\vec{k}$ est $4\pi k^{2}dk$ (c'est le volume compris entre deux sphères de rayons

), le volume d'une cellule élémentaire de cet espace est:

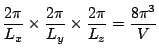
$\displaystyle \frac{2\pi}{L_{x}}\times\frac{2\pi}{L_{y}}\times\frac{2\pi}{L_{z}} = \frac{8\pi^{3}}{V}$

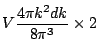$\displaystyle \left. \rho(k)dk \right.$	$\displaystyle =$	$\displaystyle V\frac{4\pi k^{2}dk}{8\pi^{3}}\times 2$
	$\displaystyle =$	$\displaystyle \frac{V}{\pi^{2}}k^{2}dk$
	$\displaystyle =$	$\displaystyle \rho(\omega)d\omega ~~~~~~$ d'autre part

$\displaystyle \fbox{$\displaystyle \rho(\omega) = \frac{V}{\pi^{2}c^{3}}\omega^{2}$}$

(9.1)

Intéressons-nous à présent à l'hamiltonien total du système. Nous admettrons que les photons n'interagissent pas entre eux, et qu'à chaque mode propre du champ électromagnétique de la cavité l'on associe un oscillateur harmonique quantique à une dimension:

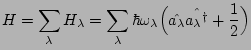$\displaystyle H = \sum_{\lambda}{H_{\lambda}} = \sum_{\lambda}{\hbar\omega_{\lambda}\Big(\hat{a_{\lambda}}\hat{{a_{\lambda}}^{\dag }} + \frac{1}{2}\Big)}$

(9.2)

Le spectre des énergies propres est donc quantifié: au mode propre $\lambda$ correspond une énergie propre $\hbar\omega_{\lambda}\Big(N_{\lambda} + \frac{1}{2}\Big)$ . L'énergie totale du champ électromagnétique est donc:

$\displaystyle E({N_{\lambda}}) = \sum_{\lambda}{\frac{\hbar\omega_{\lambda}}{2}} + \sum_{\lambda}{\hbar N_{\lambda}\omega_{\lambda}}$

Nous effectuons comme d'habitude une translation de l'échelle des énergies et prenons pour origine des énergies celle du niveau fondamental. L'énergie totale du champ est donc:

$\displaystyle E({N_{\lambda}}) = \sum_{\lambda}{\hbar N_{\lambda}\omega_{\lambda}}$

(9.3)

Dès lors, les états propres de l'hamiltonien du gaz de photons sont décrits par la configuration des $\{N_{\lambda}\}$ . Il s'ensuit généralement un changement de langage afin de décrire les niveaux énergétiques du champ quantifié:

Plus généralement, $N_{\lambda}$ est le nombre de photons présents dans l'état individuel $\lambda$ .

Reste maintenant à définir le spin du photon. Celui-ci est étroitement lié aux directions de polarisation du champ électromagnétique. Comme en l'occurrence il y a deux directions de polarisation possibles par mode propre, on s'attend à ce que le nombre quantique magnétique de spin du photon ait deux valeurs possibles. Dans ce cas, la mécanique quantique nous dit que $S = \frac{1}{2}$ ! Ce qui est évidemment faux dans la mesure où le photon est un boson et non pas un fermion. On admettra en fin de compte que le spin du photon est égal à 1, donc $m_{s} = -1, 0 , 1$ . Néanmoins, le photon est ultrarelativiste et ne peut pas être au repos, la valeur $m_{s} = 0$ est impossible. En conclusion: