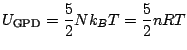Energie interne des gaz parfaits

suivant: Gaz réels monter: Théorie cinétique des gaz précédent: Définition cinétique de la Table des matières Index

Energie interne des gaz parfaits

En général, on définit l'énergie interne d'un gaz quelconque par:

$\displaystyle U = \underbrace{\sum{E_{c}}}_{\text{particules}} + \underbrace{\sum{Ep}}_{\text{interactions}}$

Or il n'y a pas d'interaction entre molécules de gaz parfaits : le second terme est nul. On distingue malgré tout deux cas :

-

celui du gaz parfait monoatomique (GPM): les molécules sont assimilées à leur centre de masse et seules les énergies cinétiques de translation sont à prendre en compte:

$\displaystyle U_{\text{GPM}} = \sum{\frac{1}{2}mv^{2}} = N<E_{c}> ~= \frac{3}{2}Nk_{B}T$

-

celui du gaz parfait polyatomique (GPP): il faut non seulement tenir compte de l'énergie cinétique de translation du centre de masse de chaque molécule de gaz, mais aussi de l'énergie cinétique barycentrique, notée $E_{c}^{*}$ , relative au mouvement désordonné des atomes dans le référentiel barycentrique $R^{*}$ de la molécule. On se contentera là encore de l'exemple du gaz parfait diatomique pour lequel se rajoutent deux degrés de rotation supplémentaires et ainsi, d'après le théorème d'équipartition de l'énergie ( $\frac{1}{2}k_{B}T$ par terme quadratique dans l'hamiltonien du système):

$\displaystyle U_{\text{GPD}} = \frac{5}{2}Nk_{B}T = \frac{5}{2}nRT$

Dans tous les cas, nous retenons que l'énergie interne d'un gaz parfait ne dépend que de la température :

$\displaystyle U_{\text{GP}} = U(T)$

(1.8)

suivant: Gaz réels monter: Théorie cinétique des gaz précédent: Définition cinétique de la Table des matières Index

Clément Baruteau 2003-04-30