Dans la section précédente, on a introduit la probabilité ![]() que le système
que le système ![]() occupe le microétat
occupe le microétat
![]() ; à présent on considère la probabilité
; à présent on considère la probabilité
![]() que
que ![]() ait l'énergie
ait l'énergie ![]() . Nous avons simplement
. Nous avons simplement
![]() où
où
![]() est le degré de dégénérescence de l'énergie
est le degré de dégénérescence de l'énergie ![]() . D'où:
. D'où:
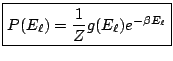 |
(4.6) |
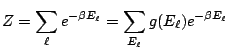 |
(4.7) |
Dans le cas où le système étudié ![]() est macroscopique - ce qui n'empêche pas de vérifier
est macroscopique - ce qui n'empêche pas de vérifier
![]() - les microétats occupés correspondent à des énergies extrêmement proches si bien que l'on peut traiter l'énergie de
- les microétats occupés correspondent à des énergies extrêmement proches si bien que l'on peut traiter l'énergie de ![]() comme une variable continue et non plus discrète. La probabilité pour que l'énergie de
comme une variable continue et non plus discrète. La probabilité pour que l'énergie de ![]() soit comprise entre
soit comprise entre ![]() et
et ![]() est alors:
est alors:
La relation de normalisation
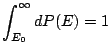 induit l'expression de la fonction de partition du système supposé macroscopique:
induit l'expression de la fonction de partition du système supposé macroscopique:
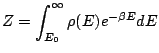 |
(4.9) |