Description d'un système macroscopique

Par système macroscopique, on entend ici un système constitué d'un très grand nombre de particules. La description d'un tel système passe par la détermination de l'hamiltonien qui régit son évolution. Or, si notre système est complexe, l'énergie potentielle d'interaction entre toutes ses particules est elle aussi complexe. Voilà pourquoi on ne peut pas déterminer l'hamiltonien exact $H_{\text{ex}}$ d'un système macroscopique.

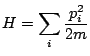La méthode est toujours la même: on commence par construire un hamiltonien approché, noté $H$, qui décrit l'essentiel des champs de forces et des liaisons imposés au système. Par exemple, pour un gaz quelconque contenu dans une enceinte, on utilisera en première approximation le modèle du gaz parfait, ainsi: $$H = \sum_i {\frac{p_i^2}{2m}}$$. Ensuite, on affine le modèle en tenant compte d'éventuelles perturbations - forces non-conservatives notament - qui constituent un hamiltonien de perturbation noté $W$: $H_{\text{ex}} = H + W$.

Dès lors, les microétats du système sont les états propres $\phi_{\ell}$ de l'hamiltonien approché. Cependant, sous l'influence de $W$, ces états propres ne sont pas des états stationnaires mais des états pseudo-stationnaires. Par conséquent, le système n'occupe pas une fois pour toute un microétat donné mais effectue des transitions aléatoires entre microétats. Il est donc naturel de chercher à calculer la probabilté d'occupation, par le système, d'un microétat donné. Pour cela, la méthode la plus intuitive est de réaliser un très grand nombre de mesures - $N$ - afin de déterminer le nombre de fois $N(\ell)$ que le système passe par le microétat $\phi_{\ell}$. La probabilité de réalisation de ce dernier est alors:

$$P_{\ell} = \lim_{N\to\infty} {\frac{N(\ell)}{N}}$$ (2.7)

Pour décrire notre système macroscopique, nous avons besoin en plus d'outils pratiques:

-

la densité d'état $\rho(E)$: le nombre $dN(E)$ de microétats d'énergie comprise entre $E$ et $E+dE$ est donné par la relation:

$$dN(E) = \rho(E)dE$$ (2.8)

-

le nombre $\phi(E)$ de microétats d'énergie inférieure ou égale à $E$, permettant de calculer explicitement $\rho(E)$. En effet, on a:

$$\displaystyle dN(E) = \phi(E+dE) - \phi(E) = \frac{d\phi}{dE}dE = \rho(E)dE$$

d'où:

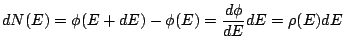
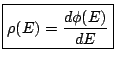$$\fbox{$\displaystyle \rho(E) = \frac{d\phi(E)}{dE}$}$$ (2.9)

Remarques:

*

signification physique de $dE$: $dE$ est un intervalle énergétique à la fois très grand devant l'échelle microscopique: $dE \gg \vert E_{\ell}-E_{\ell+1}\vert$, et très petit devant l'échelle macroscopique, représentée par l'incertitude de mesure de l'énergie.

*

de la nature d'un système macroscopique; il y a deux façons de concevoir un système macroscopique: ou bien il s'agit d'un système contenant un très grand nombre de particules, ou bien il s'agit d'un système constitué d'un petit nombre de particules mais contenu dans une ``enveloppe'' de taille macroscopique.