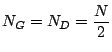Généralités

L'objectif de ce chapitre est d'introduire les raisonnements de base de la physique statistique. Il va nous falloir définir les concepts fondamentaux de microétats et de macroétats et introduire ce qu'on appelle la loi des grands nombres. En effet, le domaine de la physique statistique est celui de systèmes constitués d'un très grand nombre de particules, systèmes dont on veut décrire les propriétés thermodynamiques ou simplement l'évolution dynamique. Il serait vain de penser appliquer les règles de la mécanique classique à chacune de ces particules, dont le nombre atteint typiquement le nombre d'Avogadro. Nous allons au contraire effectuer des prédictions statistiques sur le système et nous constaterons que ces prédictions se révêlent exactes, du fait du très grand nombre de particules constituant le système.

Afin d'illustrer ces propos, nous nous proposons d'aborder la physique statistique sur un exemple introductif, celui de la détente de Joule - Gay Lussac. Nous l'avons déjà rencontrée au chapitre précédent dans le cadre de la thermodynamique classique: nous en avons fait une étude cinématique, en insistant sur l'irréversibilité de la détente. Il s'agit à présent de l'analyser d'un point de vue statistique.

Considérons ainsi une boîte macroscopique munie de parois fixes et adiabatiques, contenant de l'argon, dans les conditions usuelles de température et de pression: $T = 273,15~$K, $p = 1 ~$atm, $V = 22,4 ~$L; le nombre de particules de gaz à l'intérieur de la boîte est ainsi égal au nombre d'Avogadro: $N = N_A$. Comme au chapitre précédent, notre boîte est initialement divisée en deux enceintes de même volume, séparées par une paroi adiabatique: celle de gauche contient tout le gaz et celle de droite est vide. Notons $N_G$ respectivement $N_D$ le nombre de particules de gaz dans le compartiment de gauche respectivement de droite. A l'instant initial de l'expérience - $N_G = N$ et $N_D = 0$ - nous retirons la paroi. Notre objectif est de prévoir ce que sera l'état d'équilibre final: on s'attend a priori à ce que celui-ci se caractérise par $$N_G = N_D = \frac{N}{2}$$. 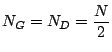Tout le problème est de savoir si cette intuition est exacte ou non, et, dans le cas défavorable, quelle est l'erreur commise.