Bilans entropiques

suivant: Entropie d'un gaz parfait monter: Second Principe de la précédent: Sources de chaleur Table des matières Index

Bilans entropiques

a)

L'univers

Il s'agit d'un système - a priori - isolé, il n'échange rien: son entropie d'échange est donc nulle. D'où $\Delta S_{\text{univers}} = S_{\text{c}_{u}} \geq 0$ . En fait, par convention, l'univers est un ``ensemble'' constitué du système étudié noté $\Sigma$ , des systèmes mécaniques parfaits notés $\Sigma^{'}$ , qui n'échangent de l'énergie que sous forme de travail, et enfin des vrais sources de chaleurs, notées , qui n'échangent de l'énergie que sous forme de chaleur.

b)

Bilans d'entropie

Pourquoi effectuer un bilan d'entropie sur un système? Essentiellement pour avoir accès à son entropie de création, qui détermine si la transformation qu'il subit est réversible ou pas. Deux cas se présentent:

-

soit le système est isolé, dans ce cas on effectue directement un bilan entropique sur le système en question.

-

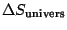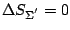soit le système n'est pas isolé, on doit effectuer un bilan d'entropie sur l'univers car seul le signe de $\Delta S_{\text{univers}}$ donne accès à l'entropie de création du système. En effet, l'extensivité de S donne: $\Delta S_{\text{u}} = \Delta S_{\Sigma} + \Delta S_{\Sigma^{'}} + \Delta S_{\text{s}}$ , avec $\Delta S_{\Sigma^{'}} = 0$ (on rappelle qu'un système mécanique parfait évolue de façon isentropique). De plus, la source de chaleur subit une transformation isotherme réversible; d'après (1.5.3), son entropie s'écrit:

$\displaystyle \Delta S_{\text{s}} = \frac{Q_{\text{s}}}{T_{\text{s}}} = -\frac{Q_{\Sigma}}{T_{\text{s}}} = -\frac{Q}{T_{\text{s}}}$

Donc

$\displaystyle \Delta S_{u} = \Delta S - \frac{Q}{T_{\text{s}}} \geq 0$

soit

$\displaystyle \Delta S \geq \frac{Q}{T_{\text{s}}}$

(1.26)

c)

Remarques

-

S'il existe plusieurs sources, on a par extension,

$\displaystyle \Delta S \geq \sum_{i}{\frac{Q_{i}}{T_{\text{s},i}}}$

(1.27)

-

Pour une pseudo source, on a par analogie,

$\displaystyle \Delta S \geq \int{\frac{\delta Q}{T}}$

(1.28)

Les trois inégalités précédentes permettent de déterminer l'inégalité de Carnot - Clausius: soit un système évoluant de façon cyclique, pour lequel $\Delta S = 0$ car est un paramètre d'état, il vient donc

$\displaystyle \fbox{$\displaystyle \frac{Q}{T_{\text{s}}} \leq 0$}$

(1.29)

On a bien entendu égalité si la transformation est réversible; les autres expressions de cette inégalité sont: $\sum_{i}{\frac{Q_{i}}{T_{\text{s},i}}} \leq 0$ (si il existe plusieurs sources) ou encore $\int{\frac{\delta Q}{T}} \leq 0$ (dans le cas d'une pseudo source).

suivant: Entropie d'un gaz parfait monter: Second Principe de la précédent: Sources de chaleur Table des matières Index

Clément Baruteau 2003-04-30