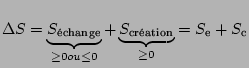Enoncé et conséquences

Le problème est le suivant: le premier principe ne fait que traduire la conservation de l'énergie mais ne permet pas de déterminer le sens d'évolution d'une transformation (réversibilité ou non par exemple). Ainsi, dans le cas de la détente de Joule - Gay Lussac, le premier principe n'interdit pas un retour du gaz détendu dans l'espace qu'il occupait avant l'ouverture du robinet, alors que le bon sens - ou plutôt l'habitude - si. D'où la nécessité d'un second principe afin de résoudre cette difficultée.

Conséquences du second principe:

-

$\Delta S_{\text{cycle}} = 0$ dans la mesure où $S$ est une fonction d'état.

-

Tout bilan d'état peut s'écrire sous la forme

$$\Delta S = \underbrace{S_{\text{échange}}}_{\geq 0 ou \leq 0} + \underbrace{S_{\text{création}}}_{\geq 0} = S_{\text{e}} + S_{\text{c}}$$

L'entropie d'échange caractérise les échanges de matière et d'énergie que peut effectuer le système avec le milieu extérieur, il s'agit donc d'une quantité positive ou négative. L'entropie de création est, elle, l'entropie créée à l'intérieur du système, pour lui-même, c'est une quantité positive ou nulle. Elle est déterminante car elle caractérise la réversibilité ou non d'une transformation: 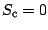$S_{\text{c}} = 0$ pour une transformation réversible, $S_{\text{c}} > 0$ pour une transformation irréversible. En outre, on remarquera que dans tous les cas $\Delta S \geq S_{\text{e}}$.

-

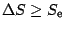Par conséquent, pour un système isolé, $S_{\text{e}} = 0$ donc $\Delta S = S_{\text{c}} \geq 0$.

-

De même, pour un système fermé, thermiquement isolé ($Q = 0$) subissant une transformation réversible, $\Delta S = 0$. Ainsi, une transformation adiabatique réversible d'un système fermé est isentropique.

L'entropie permet enfin, à l'échelle microscopique, de mesurer le degré de désordre d'un système: plus l'entropie est élevée, plus le désordre moléculaire est important.