




suivant: Relations de Mayer
monter: Capacités thermiques
précédent: Capacités thermiques
Table des matières
Index
- -
- Pour les gaz parfaits:
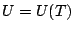 donc
donc
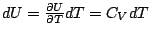 ; de même
; de même
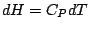 . C'est important car cela signifie que, sous l'hypothèse que les capacités thermiques ne dépendent pas du temps - voir par exemple les relations (1.19) et (1.20) ci-dessous -, les relations pratiques:
sont vraies en toutes circonstances. En outre, pour les gaz parfaits,
. C'est important car cela signifie que, sous l'hypothèse que les capacités thermiques ne dépendent pas du temps - voir par exemple les relations (1.19) et (1.20) ci-dessous -, les relations pratiques:
sont vraies en toutes circonstances. En outre, pour les gaz parfaits,
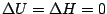 pour des transformations monothermes ou isothermes.
pour des transformations monothermes ou isothermes.
- -
- Exemple: pour les gaz parfaits monoatomiques:
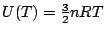 donc
donc
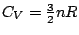 . De même,
. De même,
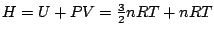 donne
donne
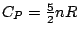 .
.
Clément Baruteau
2003-04-30