Il donne le nombre moyen de bosons dans l'état individuel défini par la donnée de son énergie
![]() , de son potentiel chimique
, de son potentiel chimique ![]() , à la température T:
, à la température T:
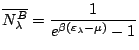 |
(8.4) |
Bien entendu, pour que
![]() , il est nécessaire que
, il est nécessaire que
![]() , énergie du niveau fondamental. Le graphe
, énergie du niveau fondamental. Le graphe
![]() suivant montre que
suivant montre que
![]() est maximal pour
est maximal pour
![]() , ce qui signifie que l'état le plus peuplé est bien le niveau fondamental.
, ce qui signifie que l'état le plus peuplé est bien le niveau fondamental.