Application

Comme application de la résonance magnétique, on traite le cas du pompage optique de type Kastler. L'objectif de ce paragraphe est de comprendre comment on détecte un phénomène de résonance magnétique et quels types d'applications ceci peut supposer.

$\rightarrow$ Transparent 14-004 qui représente un appareil de type l'appareil de Rabi. On montre en outre les électroaimants produisant $\overrightarrow {B_o}$ et $\overrightarrow {B_1}$ en transverse. La substance ici est le sodium qui est un alcalin: on se trouve dans le cadre de la RPE⁵.

La structure électronique du sodium dans son état fondamental est $1s^2~2s^2~2p^6~3s^1$: on a un électron de spin $\overrightarrow {1/2}$, de moment cinétique nul. D'où $j = 1/2$ et $m_j = \pm 1/2$. Le premier état excité de l'atome de sodium va donc correspondre à une structure électronique $1s^2~2s^2~2p^6~3p^1$: cette fois-ci, $s=1/2$ et $l=1$. Le premier état excité correspond encore au cas $j = 1/2$ et $m_j = \pm 1/2$.

On trace le diagramme énergétique de la figure 2.

Figure 2: Diagramme énergétique mis en jeu par l'expérience de pompage optique avec le sodium.

On admet que le montage permet de passer du niveau $m_j = -1/2$ de l'état fondamental au niveau $m_j = 1/2$ du premier état excité (processus dit de pompage). On explique que de ce niveau, on peut redescendre sur les deux niveaux de l'état fondamental par émission spontanée⁶ (temps caractéristique $\tau$), ou bien, par résonance paramagnétique électronique, peupler le niveau $m_j = -1/2$ du premier état excité. Calculons le nombre d'atomes se desexcitant depuis l'état peuplé par RPE:

$$dN = n \times e^{-\frac{t}{\tau}} \times P($$RPE$$) \times \frac{dt}{\tau}$$

où:

• $n$ est le nombre d'atomes parvenus sur le niveau $m_j = 1/2$ du premier niveau excité,
• $e^{-\frac{t}{\tau}}$ est la probabilité pour que ces atomes ne se desexcitent pas par émission spontanée,
• $P($RPE$)$ est la probabilité de transition par RPE, donnée par la formule de Rabi,
• $dt / \tau$ le nombre d'atomes du niveau $m_j = -1/2$ du premier état excité qui se desexcitent par émission spontanée.

  
  

On dit qu'on s'intéresse à la valeur de $N$ en régime permanent (intégrale sur $t$ de 0 à $\infty$), de quoi on déduit que l'intensité des raies de fluorescence issues de la desexcitation du niveau $m_j = -1/2$ du premier état excité vers l'état fondamental telle que:

$$I \propto \frac{{\omega_1}^2}{{\omega_1}^2 + {\Delta\omega}^2 + \frac{1}{\tau^2}}$$

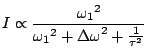
La détermination de la résonance est très précise car ce n'est qu'à la résonance ou bien très proche de celle-ci qu'on pourra détecter ces raies de fluorescence. La détermination très précise de $\omega_0 = -\gamma B_o$ permet, connaissant parfaitement⁷ $\gamma$, de mesurer $B_o$, ce qui permet de constituer des magnétomètres.