



suivant: Application
monter: Résonance magnétique
précédent: Approche classique
Table des matières
Dans cette approche, on considère la cas d'un moment magnétique de spin 1/2 qui admet deux états: un état haut +1/2 et un état bas -1/2. Ce moment magnétique de spin peut correspondre:
- au spin électronique s'il existe un nombre impair d'électrons non-appariés sur les niveaux d'énergie occupés par l'atome. Ce cas, connu des élèves, est celui de substances paramagnétiques. La résonance correspondante s'appelle Résonance Paramagnétique Electronique ou RPE. Dans ce cas, la fréquence de résonance à imposer vaut:
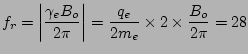 GHz à
GHz à  T.
T.
- au spin du proton, si l'on a à faire au contraire à des substance diamagnétiques. Il s'agit ici de Résonance Magnétique Nucléaire, ou RMN. La fréquence de résonance à atteindre est alors
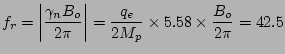 MHz à
MHz à  T, fréquence nettement plus facile à atteindre que pour la RPE.
T, fréquence nettement plus facile à atteindre que pour la RPE.
On fait interagir notre spin avec
 comme dans l'approche classique, l'instant
comme dans l'approche classique, l'instant  correspondant au spin dans l'état haut. La calcul quantique donne accès à la probabilité de mesurer à un instant
correspondant au spin dans l'état haut. La calcul quantique donne accès à la probabilité de mesurer à un instant  donné le spin dans l'état bas via la formule dite de Rabi:
donné le spin dans l'état bas via la formule dite de Rabi:
où
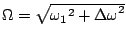 . Via le transparent 74-002, on montre bien que l'on retourve le résultat de l'approche classique, à savoir la résonance magnétique atteinte pour
. Via le transparent 74-002, on montre bien que l'on retourve le résultat de l'approche classique, à savoir la résonance magnétique atteinte pour
 , ainsi qu'une oscillation entre les deux états de spin à la pulsation caractéristique
, ainsi qu'une oscillation entre les deux états de spin à la pulsation caractéristique
 .
.




suivant: Application
monter: Résonance magnétique
précédent: Approche classique
Table des matières
baruteau clement
2005-07-18
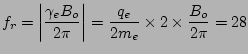 GHz à
GHz à 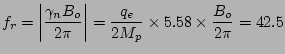 MHz à
MHz à 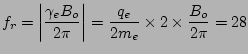 GHz à
GHz à 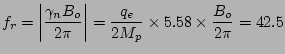 MHz à
MHz à ![]() comme dans l'approche classique, l'instant
comme dans l'approche classique, l'instant ![]() correspondant au spin dans l'état haut. La calcul quantique donne accès à la probabilité de mesurer à un instant
correspondant au spin dans l'état haut. La calcul quantique donne accès à la probabilité de mesurer à un instant ![]() donné le spin dans l'état bas via la formule dite de Rabi:
donné le spin dans l'état bas via la formule dite de Rabi:

![]() . Via le transparent 74-002, on montre bien que l'on retourve le résultat de l'approche classique, à savoir la résonance magnétique atteinte pour
. Via le transparent 74-002, on montre bien que l'on retourve le résultat de l'approche classique, à savoir la résonance magnétique atteinte pour
![]() , ainsi qu'une oscillation entre les deux états de spin à la pulsation caractéristique
, ainsi qu'une oscillation entre les deux états de spin à la pulsation caractéristique
![]() .
.