Approche classique

On part de la relation connue des élèves⁴ de proportionnalité entre le moment magnétique d'un atome et son moment cinétique total, incluant un moment cinétique orbital et un moment cinétique de spin:

$$\overrightarrow{M} = \gamma\vec{J}$$

où $\gamma$ est le facteur gyromagnétique.

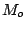- On part d'un moment magnétique orienté selon un axe $\overrightarrow{e_z}$, de norme constante $M_o$. On impose un champ magnétique statique $\overrightarrow {B_o} = B_o \overrightarrow {e_z}$: le théorème du moment dynamique donne:

$$\frac{d\overrightarrow {J}}{dt} = \overrightarrow {M} \wedge \overrightarrow {B_o} ~~$$i.e.$$~~ \frac{d\overrightarrow {M}}{dt} = \overrightarrow {\omega_0} \wedge \overrightarrow {M}$$

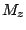où $\overrightarrow {\omega_0} = -\gamma\overrightarrow {B_o}$ est la pulsation propre de précession de notre moment magnétique autour de l'axe su champ statique. La grandeur qui nous intéresse dans ce paragraphe est la projection de $\overrightarrow {M}$ selon l'axe $\overrightarrow{e_z}$, que l'on note $M_z$. On voit que pour le moment 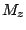$M_z$ reste constamment égale à $M_o$.

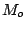- La problématique posée est: ``peut-on, à partir d'une telle configuration, parvenir à retourner $\overrightarrow {M}$?'' Pour cela on implique un champ magnétique $\overrightarrow {B_1}$ transversal à $\overrightarrow {B_o}$ et tournant à la pulsation $\omega$ (il suffit pour cela de disposer deux bobines selon (Ox) et (Oy) parcourues par un courant alternatif de pulsation $\omega$):

Figure 1: Champ magnétiques statique et transversal.

Soit R le référentiel (Oxyz) et R' le référentiel (OXYz), encore appelé référentiel de Larmor. Par analogie avec ce qui précède, on a:

$$\left(\frac{d\overrightarrow {M}}{dt}\right)_R = ( \overrightarrow {\omega_0} + \overrightarrow {\omega_1} ) \wedge \overrightarrow {M}$$

où $\overrightarrow {\omega_1} = -\gamma\overrightarrow {B_1}$. On va plutôt se placer dans le référentiel de Larmor dans lequel, après application de la formule de dérivée vectorielle, on trouve:

$$\left(\frac{d\overrightarrow {M}}{dt}\right)_{R'} = ( \overrightarrow {\omega_1} - \overrightarrow {\Delta\omega} ) \wedge \overrightarrow {M}$$

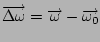où $\overrightarrow {\Delta\omega} = \overrightarrow {\omega} - \overrightarrow {\omega_0}$. On en déduit que dans ce référentiel, $\overrightarrow {M}$ précesse autour de l'axe d'un champ effectif $\overrightarrow {B_{\text{eff}}} = B_1 + \overrightarrow {\Delta\omega} / \gamma$ à la vitesse $\vert\overrightarrow {\omega_1} - \overrightarrow {\Delta\omega}\vert = \sqrt{ {\omega_1}^2 + {\Delta\omega}^2}$. 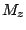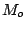Ce qui nous intéresse ici est de regarder le cas particulier où $\Delta\omega = 0$: on se retrouve dans le cas particulier où $\overrightarrow {M}$ précesse autour de l'axe du champ transversal, pour lequel $M_z$ balaie continuement au cours du temps les valeurs $-M_o$ à $M_o$, avec la pulsation caractéristique $\omega_1$. 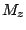C'est donc dans la situation précise où $\omega_r = \omega_0$ que l'on un mamimum de l'amplitude des variations de $M_z$, situation que l'on qualifie a fortiori de résonance. On pourra faire remarquer que la résonance magnétique est atteinte indépendamment de la valeur de $\vert\overrightarrow {B_1}\vert$.