Nous étudions dans ce chapitre ![]() particules identiques, indépendantes et indiscernables, enfermées dans un volume
particules identiques, indépendantes et indiscernables, enfermées dans un volume ![]() en contact avec un réservoir d'énergie. On suppose de plus que la limite thermodynamique est atteinte, ce qui signifie que
en contact avec un réservoir d'énergie. On suppose de plus que la limite thermodynamique est atteinte, ce qui signifie que ![]() est suffisament important afin que les fluctuations relatives des grandeurs étudiées soient négligeables devant leur valeur moyenne, mais pas trop pour que l'approximation de Maxwell-Boltzmann soit justifiée.
La fonction de partition du système total est donc:
est suffisament important afin que les fluctuations relatives des grandeurs étudiées soient négligeables devant leur valeur moyenne, mais pas trop pour que l'approximation de Maxwell-Boltzmann soit justifiée.
La fonction de partition du système total est donc:


D'après le chapitre précédent, nous savons que la condition de validité de l'approximation de Maxwell-Boltzmann est :
Effectuons un changement d'origine des énergies en prenant pour origine l'énergie du niveau fondamental : posons
![]() . La fonction de partition d'une particule devient ainsi:
. La fonction de partition d'une particule devient ainsi:
 |
|||
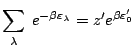 |
 |
(5.1) |
où
![]() est le degré de dégénérescence du niveau fondamental.
est le degré de dégénérescence du niveau fondamental.
On remarque aussi qu'il suffit désormais de vérifier ![]() pour valider l'approximation de Maxwell-Boltzmann .
pour valider l'approximation de Maxwell-Boltzmann .
Attention: Ce chapitre est souvent intitulé ``gaz parfait à la limite classique''. Cela ne signifie en aucune façon que l'on peut calculer ![]() par la mécanique classique, ce qui correponderait à l'approximation classique.
par la mécanique classique, ce qui correponderait à l'approximation classique.