



suivant: Résonance magnétique
monter: lliço55fisica
précédent: Résonance en électrocinétique
Table des matières
On va fonder notre propos sur l'interféromètre de Fabry-Pérot en l'assimilant à une cavité résonante à une dimension. Les hypothèses sont les suivantes:
- approximation scalaire,
- les ondes sont issues d'une source ponctuelle monochromatique,
- les miroirs sont infiniment minces, parallèles, distants de
 et identiques (mêmes coefficients de réflexion R et transmission T en intensité),
et identiques (mêmes coefficients de réflexion R et transmission T en intensité),
- incidence normale:
 .
.
Ainsi la différence de marche optique entre deux ondes émergentes vaut 2 et la différence de phase correspondante est
et la différence de phase correspondante est
 . On mène rapidement le calcul de l'amplitude résultante des ondes émergentes:
. On mène rapidement le calcul de l'amplitude résultante des ondes émergentes:
 (somme d'une série géométrique) puis directement l'expression de l'intensité est:
(somme d'une série géométrique) puis directement l'expression de l'intensité est:
où
 . On n'a pas nécessairement R + T = 1 (absorptions possibles). Graphe de la fonction d'Airy sur T réf 14-003.
. On n'a pas nécessairement R + T = 1 (absorptions possibles). Graphe de la fonction d'Airy sur T réf 14-003.
I est maximale lorsque
 i.e. lorsque
i.e. lorsque
 , ce qui s'écrit encore sous deux formes intéressantes:
, ce qui s'écrit encore sous deux formes intéressantes:
- *
-
 , ce qui rappelle la condition d'excitation d'un mode propre de vibration pour une corde de Melde. Ceci fait le lien avec le fait qu'on a présenté le Fabry-Pérot comme une cavité résonance 1D,
, ce qui rappelle la condition d'excitation d'un mode propre de vibration pour une corde de Melde. Ceci fait le lien avec le fait qu'on a présenté le Fabry-Pérot comme une cavité résonance 1D,
- *
-
 : on interprète les conditions d'interférences constructives comme une résonance en intensité lumineuse et on conclut que, contrairement au paragraphe précédent où l'on n'avait isolé une unique pulsation de résonance3, ici il existe de nombreuses pulsations de résonance reliées entre elles de façon discrète.
: on interprète les conditions d'interférences constructives comme une résonance en intensité lumineuse et on conclut que, contrairement au paragraphe précédent où l'on n'avait isolé une unique pulsation de résonance3, ici il existe de nombreuses pulsations de résonance reliées entre elles de façon discrète.
On interprète de même les conditions d'interférences destructives comme des antirésonances du système.
Applications:
- peut-on trouver une analogie du facteur de qualité pour notre interféromètre? On est ammené à chercher une grandeur du type
 , qui n'est autre que le pouvoir de résolution du Fabry-Pérot. Par analogie avec le TP-cours de spectromètrie optique, on est tenté de définir une dispersion en différence de phase de la même façon qu'on avait introduit la dispersion en déviation angulaire:
, qui n'est autre que le pouvoir de résolution du Fabry-Pérot. Par analogie avec le TP-cours de spectromètrie optique, on est tenté de définir une dispersion en différence de phase de la même façon qu'on avait introduit la dispersion en déviation angulaire:
De plus,
 correspond à une différence de phase qui peut être résolue par l'interféromètre; elle est donc donnée par la largeur à mi-hauteur des pics de la fonction d'Airy:
correspond à une différence de phase qui peut être résolue par l'interféromètre; elle est donc donnée par la largeur à mi-hauteur des pics de la fonction d'Airy:
 . On en déduit le pouvoir de résolution par:
. On en déduit le pouvoir de résolution par:
Le premier terme est l'ordre d'interférence  , le second s'appelle un facteur de finesse
, le second s'appelle un facteur de finesse  ; il ne dépend que du facteur de réflexion
; il ne dépend que du facteur de réflexion  en intensité des miroirs. On conclut par les AN du T réf 14-003 sur l'utilité d'un tel système en spectroscopie.
en intensité des miroirs. On conclut par les AN du T réf 14-003 sur l'utilité d'un tel système en spectroscopie.
- On peut parler de la fabrication des filtres interférentiels qui sont des lames diélectriques à faces parallèles, partiellement réfléchissantes, ne transmettant qu'une petite bande
 du rayonnement incident autour d'une longueur d'onde de ``travail''
du rayonnement incident autour d'une longueur d'onde de ``travail''  . On peut donc légitimement les assimiler à des cavités de type Fabry-Pérot enserrant un milieu d'indice
. On peut donc légitimement les assimiler à des cavités de type Fabry-Pérot enserrant un milieu d'indice 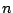 . Par analogie avec ce qui précède, la condition de résonance est donnée par
. Par analogie avec ce qui précède, la condition de résonance est donnée par
 . On s'arrange en pratique pour que
. On s'arrange en pratique pour que
 avec
avec  afin que les autres longueurs d'onde qui satisfont à la condition de résonance n'appartiennent pas au domaine du visible (
afin que les autres longueurs d'onde qui satisfont à la condition de résonance n'appartiennent pas au domaine du visible (
 ). Ainsi pour
). Ainsi pour
 nm (raie verte du mercure), on a
nm (raie verte du mercure), on a
 nm, loin dans l'UV.
Quid de la largeur
nm, loin dans l'UV.
Quid de la largeur
 ? D'après ce qui précède, on aura:
AN: pour
? D'après ce qui précède, on aura:
AN: pour
 nm et
nm et  , on trouve
, on trouve
 nm, ce qui est typiquement l'ordre de grandeur auquel on s'attend. En tous cas, on voit que
nm, ce qui est typiquement l'ordre de grandeur auquel on s'attend. En tous cas, on voit que
 est d'autant plus petit que
est d'autant plus petit que  est proche de 1, ce qui justifie l'utilisation de plusieurs couches de diéléctriques pour parvenir à nos fins...
est proche de 1, ce qui justifie l'utilisation de plusieurs couches de diéléctriques pour parvenir à nos fins...
- On vient de considerer en quelque sorte le Fabry-Pérot comme un filtre passe-bande multi-bande. On peut donc citer comme autre utilisation celle de la sélection de modes d'un laser. En effet on peut modélier un laser par une cavité résonante avec des modes longitudinaux distants de
 où
où  est la longueur optique de la cavité. AN: pour
est la longueur optique de la cavité. AN: pour  cm, on trouve des modes distants de 0.5 GHz. Pour sélectionner un mode, il nous faudra un pouvoir de résolution théorique
cm, on trouve des modes distants de 0.5 GHz. Pour sélectionner un mode, il nous faudra un pouvoir de résolution théorique
 . Un tel pouvoir de résolution est en théorie largement atteignable d'après ce qu'on a vu précédemment avec l'interféromètre de Fabry-Pérot. Mais il faut nuancer car en pratique on sera limité par les défauts de planéïté des miroirs!
. Un tel pouvoir de résolution est en théorie largement atteignable d'après ce qu'on a vu précédemment avec l'interféromètre de Fabry-Pérot. Mais il faut nuancer car en pratique on sera limité par les défauts de planéïté des miroirs!
- On vient de traiter le cas de cavités résonantes 1D, on embraye sur la modélisation d'un pont (
 corde de Melde large) comme cavité 2D avec transparent 15-001 pour celui de Tacoma (torsion selon la largeur, flexion selon la longueur). On termine enfin cette partie avec une cavité 3D: le fréquencemètre embarqué sur le guide d'ondes (
corde de Melde large) comme cavité 2D avec transparent 15-001 pour celui de Tacoma (torsion selon la largeur, flexion selon la longueur). On termine enfin cette partie avec une cavité 3D: le fréquencemètre embarqué sur le guide d'ondes (
 manip). La manip est rapide: on part de la cavité résonante fermée et en position de ventre de vibration de l'enveloppe du champ électrique via l'antenne. On ouvre la cavité résonante jusqu'à ce que l'on constate une absorption de l'énergie par la cavité ainsi accordée. On arrive ainsi à une autre définition de la résonance comme maximum d'énergie absorbée par le système.
manip). La manip est rapide: on part de la cavité résonante fermée et en position de ventre de vibration de l'enveloppe du champ électrique via l'antenne. On ouvre la cavité résonante jusqu'à ce que l'on constate une absorption de l'énergie par la cavité ainsi accordée. On arrive ainsi à une autre définition de la résonance comme maximum d'énergie absorbée par le système.




suivant: Résonance magnétique
monter: lliço55fisica
précédent: Résonance en électrocinétique
Table des matières
baruteau clement
2005-07-18
![]() et la différence de phase correspondante est
et la différence de phase correspondante est
 . On mène rapidement le calcul de l'amplitude résultante des ondes émergentes:
. On mène rapidement le calcul de l'amplitude résultante des ondes émergentes:
 (somme d'une série géométrique) puis directement l'expression de l'intensité est:
(somme d'une série géométrique) puis directement l'expression de l'intensité est:

 . On n'a pas nécessairement R + T = 1 (absorptions possibles). Graphe de la fonction d'Airy sur T réf 14-003.
. On n'a pas nécessairement R + T = 1 (absorptions possibles). Graphe de la fonction d'Airy sur T réf 14-003.
![]() i.e. lorsque
i.e. lorsque
![]() , ce qui s'écrit encore sous deux formes intéressantes:
, ce qui s'écrit encore sous deux formes intéressantes:
 , ce qui rappelle la condition d'excitation d'un mode propre de vibration pour une corde de Melde. Ceci fait le lien avec le fait qu'on a présenté le Fabry-Pérot comme une cavité résonance 1D,
, ce qui rappelle la condition d'excitation d'un mode propre de vibration pour une corde de Melde. Ceci fait le lien avec le fait qu'on a présenté le Fabry-Pérot comme une cavité résonance 1D,
 , qui n'est autre que le pouvoir de résolution du Fabry-Pérot. Par analogie avec le TP-cours de spectromètrie optique, on est tenté de définir une dispersion en différence de phase de la même façon qu'on avait introduit la dispersion en déviation angulaire:
, qui n'est autre que le pouvoir de résolution du Fabry-Pérot. Par analogie avec le TP-cours de spectromètrie optique, on est tenté de définir une dispersion en différence de phase de la même façon qu'on avait introduit la dispersion en déviation angulaire:
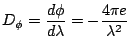
![]() correspond à une différence de phase qui peut être résolue par l'interféromètre; elle est donc donnée par la largeur à mi-hauteur des pics de la fonction d'Airy:
correspond à une différence de phase qui peut être résolue par l'interféromètre; elle est donc donnée par la largeur à mi-hauteur des pics de la fonction d'Airy:
 . On en déduit le pouvoir de résolution par:
. On en déduit le pouvoir de résolution par:
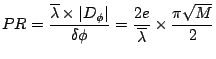
![]() , le second s'appelle un facteur de finesse
, le second s'appelle un facteur de finesse ![]() ; il ne dépend que du facteur de réflexion
; il ne dépend que du facteur de réflexion ![]() en intensité des miroirs. On conclut par les AN du T réf 14-003 sur l'utilité d'un tel système en spectroscopie.
en intensité des miroirs. On conclut par les AN du T réf 14-003 sur l'utilité d'un tel système en spectroscopie.
 . On s'arrange en pratique pour que
. On s'arrange en pratique pour que
